Representing Quantum Gates in Tensor Product Space

[phun_physics]

TL;DR Summary

I am confused on how to represent the computational (matrix) form of a quantum gate in the tensor product space. For example: how does the computational matrix look for a single qubit gate on in two qubit tensor product vector space?

Where do I start. I want to write the matrix form of a single or two qubit gate in the tensor product vector space of a many qubit system. Ill outline a simple example:

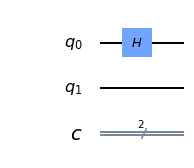
Both qubits, $q_0$ and $q_1$ start in the ground state, $|0 \rangle =\begin{pmatrix}1 \\ 0 \end{pmatrix}$. Then we apply the Hadamard gate, $\begin{pmatrix} 1 & 1 \\ -1 & 1 \end{pmatrix}$, on the $q_0$.
Here is my understanding:

The Hadamard gate on two qubit system only operates on $q_0$
$$ \hat{H}_0(q_0 \otimes q_1) = \hat{H}_0q_0 \otimes q_1 $$
$$\hat{H}_0(|0 \rangle \otimes |0 \rangle) = \hat{H}_0|0\rangle \otimes |0\rangle$$
$$\hat{H}_0 (\begin{pmatrix} 1 \\ 0 \end{pmatrix} \otimes \begin{pmatrix} 1 \\ 0 \end{pmatrix} )= \hat{H}_0 \begin{pmatrix} 1 \\ 0 \end{pmatrix} \otimes \begin{pmatrix} 1 \\ 0 \end{pmatrix}$$
$$\hat{H}_0 \begin{pmatrix} 1 \\ 0 \\ 0 \\0 \end{pmatrix} = \frac{1}{\sqrt{2}} ( \begin{pmatrix} 1 \\ 1 \end{pmatrix} \otimes \begin{pmatrix} 1 \\ 0 \end{pmatrix})$$
$$\hat{H}_0 \begin{pmatrix} 1 \\ 0 \\ 0 \\0 \end{pmatrix} = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 \\ 0 \\ 1 \\ 0 \end{pmatrix}$$

I don't know exactly how to solve this but can give a guess.

$$\hat{H}_0 = \begin{pmatrix} 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \\
1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix}$$

How is $\hat{H}_0$ written in the tensor product space? Are there any resources that explain this well? Any help is appreciated!

 

[DrClaude]

What you have is the tensor product of two matrices, such that what you call $\hat{H}_0$ is actually $\hat{H}_0 \otimes \hat{I}_1$, where $\hat{I}_1$ is the identity operator acting on $q_1$. That product can easily be calculated, see https://mathworld.wolfram.com/KroneckerProduct.html