Can I Rescale These Bottle Design Functions for Half the Volume?

[BigKevSebas]

All variables and given/known data and Relevant equations:
So I got the functions for a bottle design (one side with the bottle lying horizontally):
1. y=-1/343x^3+3/98x^2 + 2.5 ; 0<x<7
2. y=3; 7<x<15
3. y=-1/98x^2+15/49x+69/98; 15<x<22
Combined they give the volume of 570.2mL using the volume revolution equation:

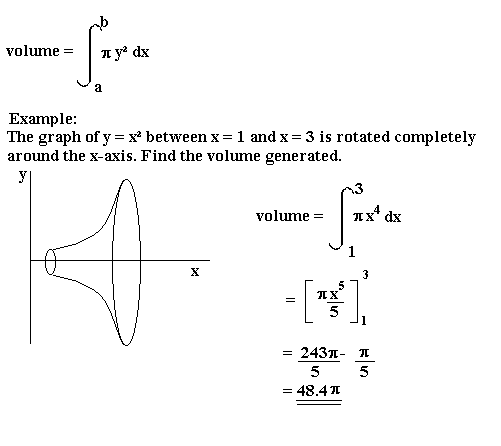
I need to rescale the functions above so that I get half the volume. I simply can't reduce the length of the functions by half, as the new curves have to be a similar shape to the original one. Therefore I need to reduce the radius and length at the same time.

The attempt at a solution
I know I have to multiply the function by 1/2^(1/3). To do this I had to convert function 3 to the vertex form, and I got

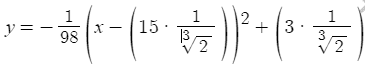, as the new rescaled function 3.
Furthermore, I also got,

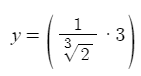as the new function of 2.

The problem:
I'm stuck on rescaling function 1, as I can't convert it to a vertex form. I have tried the method from 'https://www.enotes.com/homework-help/how-convert-cubic-equation-standard-form-ax-2-bx-2-312067' but that has not worked. Any ideas how I would be able to rescale function 1.

 

[scottdave]

Why are you dividing by cube root of 2? If you keep the horizontal length constant, dividing radius by square root of 2 should have the desired result of cutting the cross sectional area in half (which will cut the volume in half).

 

[scottdave]

I don't understand why you need to convert the function to another form.
If you have y = f(x) from x=15 to 22 and that has a certain volume by integrating πy²dx from x=15 to 22,
Why can't your new function just be y = f(x)/(√2) ? Since it is a polynomial, that is just dividing each term by (√2)
Same with the other pieces.

 

[Ray Vickson]

I don't understand why you need to convert the function to another form.
If you have y = f(x) from x=15 to 22 and that has a certain volume by integrating πy²dx from x=15 to 22,
Why can't your new function just be y = f(x)/(√2) ? Since it is a polynomial, that is just dividing each term by (√2)
Same with the other pieces.

I think he wants to scale both x and y by the same factor, so that the "shape" remains the same.

 

[LCKurtz]

The OP probably should have put this as a continuation of this thread:
https://www.physicsforums.com/threads/water-bottle-design-using-polynomials.921665/
instead of starting a new thread on the topic.

 

[BigKevSebas]

Sorry, I am new. But yes I want to scale both x and y by the same factor so that the "shape" remains the same.The task requires the rescaling of the bottle to have a similar shape of the original.

 

[scottdave]

I want to scale both x and y by the same factor so that the "shape" remains the same.The task requires the rescaling of the bottle to have a similar shape of the original.

That makes more sense now

 

[LCKurtz]

Sorry, I am new. But yes I want to scale both x and y by the same factor so that the "shape" remains the same.The task requires the rescaling of the bottle to have a similar shape of the original.

What I showed in this post in your other thread:
https://www.physicsforums.com/threads/water-bottle-design-using-polynomials.921665/#post-5815215
was a method to do your problem. You could use it. Your original functions would all be in terms of $h$ and you could scale it just by changing $h$.

 

[scottdave]

One way to achieve what @LCKurtz suggests, using your current formulas, is to make a g(x) which is equal to {f(x*2^(-1/3))}*2^(-1/3), then you need to change each limit of x range to {x_limit}*2^(-1/3), where x_limit is a lower limit or upper limit for each range.

Another thing, I thought your original problem was to achieve 600 cubic centimeters (mL), but you state that you got 570.2 mL. Shouldn't you scale up to 600 first, then you can scale to half volume?

 

[BigKevSebas]

The water bottle can be 10% below or over 600mL

 

[LCKurtz]

You haven't shown us anything about your design or how you came up with the equations that you want to scale. So I am going to give you one more example of how you might approach your problem. You are probably familiar with a typical cubic, such as one that has roots at $x=0,~1,~2$ whose equation would be given by $y =A(x)(x-1)(x-2)$. The graph has a couple of arches. The constant $A$ determines the sign and how tall the arches are. So for my example, I'm going to say you want a cubic like that, with zeroes equally spaced, the first zero at $x=0$, the others positive and equally spaced, and each arch height $h$ at its midpoint (this isn't quite the max point). And you want it to be scalable so it looks the same regardless of its size. Now, to get the zeroes equally spaced to make it scalable let's put the zeroes at $0, ~h,~ 2h$. So the equation would look like this so far: $y=Ax(x-h)(x-2h)$. Now, if we want the first arch to be positive and be equal to the width of the arches, we need $y = h$ when $x = \frac h 2$. So let's put that in the equation for $y$ given above to determine $A$. This gives$$
h = A\frac h 2 (\frac h 2 - h)(\frac h 2 -2h) = A(\frac h 2)(-\frac h 2)(-\frac {3h} 2) = \frac 3 8 Ah^3$$
This gives $A=\frac 8 {3h^2}$ and our final scalable equation for $y$ is$$
y = \frac 8 {3h^2}(x)(x-h)(x-2h)$$Now you have everything scalable in terms of $h$. Below is a graph showing what the cubics look like for $h=1,~ h=2,~ h= 3$. Three different equations, three different sizes, but the same shape.

[Edit:] Apparently the general case is pretty easy. If you have an equation $f(x,y) = 0$ and you want to resize its graph by a factor of $k$, just use $f(\frac x k,\frac y k)=0$.