Resistance of three-dimensional objects

[Jan05]

Homework Statement

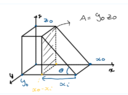
Calculate the resistance in the $x$-direction

Relevant Equations

$R = \rho ~ \frac{l}{A}$

I'm working on the following differential resistance problem and wondering wether I'm approaching the question the right way. The problem is to find an expression for the resistance in the $x$-direction of a wire with electrical resistivity $~ \rho ~$ in terms of $~ z_0 ~$, $y_0 ~$, $x_0 ~$ and $~ \theta$. I approached it the following way:

We can write $x_i$ in terms of the given variables as:

$$
x_i = \frac{z_0}{tan ~ \theta}
$$

Then add the contribution to the resistance of the two shapes together where we can write the contribution of the prism as an integral:

$$
R = \rho ~ \frac{l}{A} = \rho ~ ( \frac{x_0 - x_i}{y_0 z_0} + \int_{x_0 - x_i} ^{x_0} \frac{dx}{\frac{1}{2} x z_0})
$$

And finally:

\begin{equation}
R = \rho ~ ( \frac{x_0}{y_0 z_0} - \frac{z_0}{z_0 y_0 ~ tan ~ \theta} + \frac{2}{z_0} ~ ln ~ \frac{x_0}{x_0 - x_i}) = \rho ~ ( \frac{x_0}{y_0 z_0} - \frac{1}{y_0 ~ tan ~ \theta} + \frac{2}{z_0} ~ ln ~ \frac{x_0 ~ tan ~ \theta}{x_0 ~ tan ~ \theta - x_0})
\end{equation}

 

[kuruman]

First of all, your final equation is dimensionally incorrect and, therefore, cannot be correct.

Secondly, you approach for finding the resistance of the prism is incorrect. Please explain what exactly you are adding continuously when you write $$ \int_{x_0 - x_i} ^{x_0} \frac{dx}{\frac{1}{2} x z_0}$$ You might consider answering the following questions

1. What is the direction of the current?
2. What is the element of area perpendicular to that direction?
3. If you are adding elements $dR$, are they in series or in parallel?

 

[Jan05]

Thank you for your answer. I think I see where i made a mistake. The direction of the current is along the $x$-axis. Because the height of the prism change in function of $x$ I thought of calculating the contribution by an integral and then integrate with respect to $x$. I think that the cross-sectional area $A$ has to be $A = y_0 x ~ tan ~ \theta$ and therefore the integral becomes
$$
\int_{x_0 - x_i}^{x_0} \frac{dx}{y_0 x ~ tan ~ \theta} = \frac{1}{y_0 ~ tan ~ \theta} ~ ln ~ \frac{x_0}{x_0 - x_i}
$$

Which results in the right dimension for $R$ when being multiplied with $\rho$.

 

[kuruman]

Thank you for your answer. I think I see where i made a mistake. The direction of the current is along the $x$-axis. Because the height of the prism change in function of $x$ I thought of calculating the contribution by an integral and then integrate with respect to $x$. I think that the cross-sectional area $A$ has to be $A = y_0 x ~ tan ~ \theta$ and therefore the integral becomes
$$
\int_{x_0 - x_i}^{x_0} \frac{dx}{y_0 x ~ tan ~ \theta} = \frac{1}{y_0 ~ tan ~ \theta} ~ ln ~ \frac{x_0}{x_0 - x_i}
$$

Which results in the right dimension for $R$ when being multiplied with $\rho$.

You answered only one my three questions without bothering to answer the other two. Yes, I agree that the current is in the $x$-direction. What about an area element perpendicular to that direction? You say it is $dA= y_0 x \tan\theta$. Make a drawing and convince yourself that it is so. Then we will consider the third question.

 

[Jan05]

It isn't true that I didn't bother answering the two other questions. I gave my thoughts on the area perpendicular to the current after I worked this out on paper. For your third question: if elements $dR$ are in series we can add them together. This is what we are doing by evaluating the integral.

 

[kuruman]

It isn't true that I didn't bother answering the two other questions. I gave my thoughts on the area perpendicular to the current after I worked this out on paper. For your third question: if elements $dR$ are in series we can add them together. This is what we are doing by evaluating the integral.

Maybe you answered the questions to yourself but you didn't post the answers. I should clarified that I expected you to post the answers.. The reason for posting that is to verify that they are correct. Your answer to the area perpendicular to the current is incorrect. It cannot be $dA= y_0 x \tan\theta$ because it cannot contain $x$. It must be an area perpendicular to the $x$ direction and cannot contain length $x$.

Like I said, make a drawing of a typical element that you are adding. It would help if you posted it so that we can talk about it in case it is incorrectly drawn.

 

[Jan05]

I thought it needed to invlove $x$ because the area changes in function of $x$ so you start with the area perpendicular to the $x$-direction $A = y_0 z_0$ and then integrate in the same direction as the current from $x_0 - x_i$ to $x_0$.

 

[berkeman]

Maybe I'm being dumb, but what is the height of the area at $x_0$? This seems problematic to me...

 

[kuruman]

I thought it needed to invlove $x$ because the area changes in function of $x$ so you start with the area perpendicular to the $x$-direction $A = y_0 z_0$ and then integrate in the same direction as the current from $x_0 - x_i$ to $x_0$.

If you are going to add rectangular resistor elements in series along $x$, what is the area of one such element at position $x$ as shown below? What is its resistance $dR$? What are your limits of integration?

 

[bob012345]

Homework Statement: Calculate the resistance in the $x$-direction
Relevant Equations: $R = \rho ~ \frac{l}{A}$

View attachment 345776

I think the statement of the problem is problematic. Can you provide the exact wording of the problem and if it mentions where the contacts are? Thanks.

 

[haruspex]

I think the statement of the problem is problematic. Can you provide the exact wording of the problem and if it mentions where the contacts are? Thanks.

The only way I can see the question makes sense is if the face in the YZ plane is at one voltage and the sloping face on the right is at the other voltage.
That said, it seems to me a very difficult question. What is the path of the current?
It would be everywhere normal to the equipotential; in particular, normal to the contact faces, so it must curve upwards to meet the sloping face.
Taking it always to be parallel to the x axis will give an answer, but surely higher than the real result.