Direction of dipole moment in e-field of another dipole

[JulienB]

Homework Statement

Hi everybody! I'm trying to solve a problem about dipoles, but there is something I don't quite get about it. Well, first here is the problem:

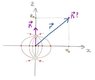
An electric dipole $\vec{p}_1$ is placed at the zero-point and shows in the z-direction. A second electric dipole $\vec{p}_2$ is placed at location $(x_0, 0, y_0)$. In which direction does the dipole $\vec{p}_2$ show in the electric field of $\vec{p}_1$?

Homework Equations

Dipole moment: $\vec{p} = q \cdot \vec{d}$
Potential of a dipole: $\phi (\vec{r}) = k \cdot \frac{\vec{r} \cdot \vec{p}}{r^3}$
Electric potential energy of a dipole: $W_{pot} = - \vec{p}_2 \cdot \vec{E}$
Electric field: $\vec{E} (\vec{r}) = - \nabla \phi (\vec{r})$

The Attempt at a Solution

People who've read me before on this forum know that I loooove to draw a picture of the problems, so I've attached one as usual to this post. To solve the problem, my thinking was the following:

I know that the potential energy of $\vec{p}_2$ will be minimal when it reaches its most stable position with respect to the electric field $\vec{E}_1$ of $\vec{p}_1$ at position $\vec{r}$. That is, $W_{pot} = - \vec{p}_2 \cdot \vec{E}_1 (\vec{r})$ will be minimal when $\vec{p}_2$ is parallel to $\vec{E}_1(\vec{r})$.

In order to find what $\vec{E}_1 (\vec{r})$ is, I first calculate the potential of $\vec{p}_1$ at position $\vec{r}$ and get:

$\phi_1 (\vec{r}) = k \cdot \frac{\vec{r} \cdot \vec{p}}{r^3} = k \cdot \frac{z_0 \cdot p_z}{(x_0^2 + z_0^2)^{3/2}}$

since $p_x = p_y = y_0 = 0$. Then the electric field of $\vec{p}_1$ is simply:

$\vec{E}_1 (\vec{r}) = - \nabla \phi_1 (\vec{r}) = (3k \cdot x_0 \cdot z_0 \cdot p_z \cdot r^{-5}, 0, 3k \cdot z_0^2 \cdot p_z \cdot r^{-5})$
$= 3k \cdot z_0 \cdot p_z \cdot r^{-5} \cdot (x_0, 0, z_0)$
$= 3k \cdot z_0 \cdot p_z \cdot r^{-5} \cdot \vec{r}$

And here comes a big surprise to me: $\vec{E}_1 (\vec{r})$ seems to be parallel to $\vec{r}$! How is that possible? When I look at the picture I drew, that can't be true. Where is my mistake?

I'm looking forward to reading you, thanks a lot in advance for your answers.Julien.

 

[JulienB]

Maybe I have found my mistake. Could it be that I have to consider two superposing electric fields, one created by the positive charge and one created by the negative charge and add them up?

Edit: Aah probably not since I use the definitions for $\vec{p}$ and not for $\vec{d}$ (distance between the two charges)...

 

[TSny]

A second electric dipole $\vec{p}_2$ is placed at location $(x_0, 0, y_0)$.

$(x_0, 0, y_0)$ ⇒ $(x_0, 0, z_0)$?

$\phi_1 (\vec{r}) = k \cdot \frac{\vec{r} \cdot \vec{p}}{r^3} = k \cdot \frac{z_0 \cdot p_z}{(x_0^2 + z_0^2)^{3/2}}$

$\vec{E}_1 (\vec{r}) = - \nabla \phi_1 (\vec{r}) = (3k \cdot x_0 \cdot z_0 \cdot p_z \cdot r^{-5}, 0, 3k \cdot z_0^2 \cdot p_z \cdot r^{-5})$

The z-component of $E_1$ is incomplete. Note that $z_0$ occurs in both the numerator and denominator of $\phi_1$.

 

[JulienB]

Hi @TSny and thanks for your answer. Oh right... That's unfortunately one of my common mistakes -_- Thanks for pointing that one out!

Julien.