Restrictions on the frame of reference

[yucheng]

Homework Statement

N/A

Relevant Equations

N/A

Newton's laws only hold in intertial frames. In general, the center of mass (CM) is accelerating, so it cannot be used as a frame. However,

1. Suppose that CM is accelerating only in the $\hat{z}$ direction. Does this mean that the CM frame is still valid in the $\hat{x}$ and $\hat{y}$ direction?

2. For rotation, suppose we want to find the torque about the CM, and the CM is acclerating in the $\hat{x}$ direction. We find that a torque about CM as origin, $\tau = f \hat{z}$ Is this then a valid frame of reference for torques as long as they are not in the same direction as the acceleration?

Context(Kleppner and Kolenkow, Problem 7.6:

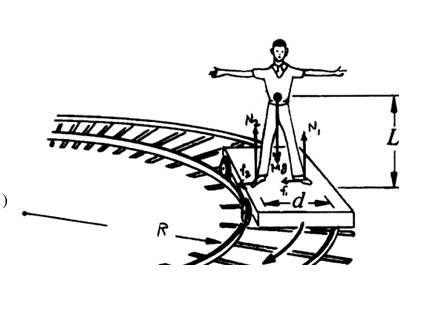
So the author found the torques around the CM (the black dot), and since the person is moving around a circular track, there is a centripetal acceleration acting on the CM, and so it should not be inertial.P.S. actually, any point that is accelerating with the conditions given, not just CM.

Thanks in advance!

 

[haruspex]

the author found the torques around the CM

It is not clear to me from your post which frame of reference the author is using. Finding a torque about the CM can be done in either.
I do not have a copy of the book you cite.

 

[yucheng]

It is not clear to me from your post which frame of reference the author is using. Finding a torque about the CM can be done in either.
I do not have a copy of the book you cite.

The big dot at the person's stomach.

All the torques are taken with respect to that dot

 

[haruspex]

The big dot at the middle

All the torques are taken with respect to that dot

The author is taking moments about the CM (big black dot), but that does not imply the author is taking the 3D person as the reference frame. You can choose a static frame with origin at the person's CM at some instant; or you could choose a non inertial frame which is anchored to the CM, so orbits the centre of curvature of the track, but does not rotate relative to the ground frame.
Whichever, any fictitious forces act at the CM, so do not affect the torque about there. In all cases, the torque from the difference in the two normal forces balances the torque from the frictional forces.

 

[bestdanny]

I didn't even expect to receive so much interesting information. Very interesting forum