Resultant forces of coplanar systems

[SUCRALOSE]

Homework Statement

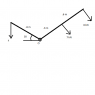
Determine the magnitude of F if the resultant of the three forces passes through point O.

Homework Equations

ƩFx = 0
ƩFy = 0
ƩM = 0

The Attempt at a Solution

The most I can come up with is that the two forces on the left would equal F on the right, and trying to ratio the force and distance it still does not work.

Any hints would be greatly appreciated.

 

[SUCRALOSE]

540 views and no one person on here can even throw a simple hint my way... I am at a loss as to why. I read the rules and have done everything instructed. What's the deal here?

 

[Doc Al]

Can you explain the diagram a bit. Is it some rigid structure that is in equilibrium?

 

[phlstr]

If it's in equilibrium, I think you can sum up moments at O and resolve F to its x and y components and find the moment due to each component. Or you could just sum up forces along x and y to 0 (but since there's no angle I think you should use the moment method).

**Just noticed you need the resultant force.. I think you should use Varignon's theorem.

 

[SUCRALOSE]

Thanks for the replies,

The question states, "determine the magnitude of the vertical force F if the resultant of the three forces acting on the crank passes through the bearing O."

So if it's a crank and the resultant is passing through a bearing then it is not in equilibrium, I am assuming.

I have tried summing the forces on the right side and converting that into it's x & y coordinates, but that does not work. I have worked out all angles and have tried lots, but nothing has worked.

The answer is 19.9 kN, just can seem to find out how to get to that.

 

[BruceW]

You're right, its not necessarily in equilibrium. Luckily, you don't need to know if its in equilibrium to answer the question. The key is in the definition of the resultant force (which I just looked up to try to get my head round it). The question says that the resultant force passes through O, so what does this tell us about the sum of the moments around O?