MHB Rickkyredu's question at Yahoo Answers (shell method for solid of revolution)

[MarkFL]

Here is the question:

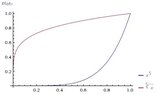
Shell method calculus?

Use the Shell Method to compute the volume of the solid obtained by rotating the region in the first quadrant enclosed by the graphs of the functions y=x^{5} and y=sqrt[5]{x} about the y-axis.

Here is a link to the question:

Shell method calculus? - Yahoo! Answers

I have posted a link there to this topic so the OP may find my response.

 

[MarkFL]

Hello Rickkyredu,

The first thing I like to do in these problems, is look at a graph of the region to be rotated:

View attachment 607

Next, I like to compute the volume of 1 arbitrary shell:

$\displaystyle dV=2\pi rh\,dx$

where:

$\displaystyle r=x,\,h=x^{\frac{1}{5}}-x^5$

and so we have:

$\displaystyle dV=2\pi x\left(x^{\frac{1}{5}}-x^5 \right)\,dx=2\pi\left(x^{\frac{6}{5}}-x^6 \right)\,dx$

Next, we need to find the limits of integration, i.e., the $x$-cooridnates of the points of intersection for the two curves:

$\displaystyle x^{\frac{1}{5}}=x^5$

$\displaystyle x^{\frac{1}{5}}-x^5=0$

$\displaystyle x^{\frac{1}{5}}\left(1-x^{\frac{4}{5}} \right)=0$

We can see then:

$x=0,\,1$

Finally, we sum up all the shells by integrating:

$\displaystyle V=2\pi\int_0^1 x^{\frac{6}{5}}-x^6\,dx=2\pi\left[\frac{5}{11}x^{\frac{11}{5}}-\frac{1}{7}x^7 \right]_0^1=2\pi\left(\frac{5}{11}-\frac{1}{7} \right)=\frac{48\pi}{77}$