Riding a Rollercoaster: Conservation of Energy, Radial Acc., & Tangential Acc.

[SpeedofSound]

Homework Statement

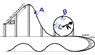
A car in an amusement park ride rolls without friction around the rack shown in homr1.gif. It starts from rest at point A at a height h above the bottom of the loop. Treat the car as a particle.

(a) What is the minimum value of h (in terms of R) such that the car moves around the loop without falling off the top (point B)?

(b) If h = 3.50R and R = 20.0m, compute the speed, radial acceleration, and tangential acceleration of the passengers when the car is at point C, which is at the end of a horizontal diameter. Show these acceleration components in a diagram, approximately to scale.

Homework Equations

K1 + U1 = K2 +U2
K1=1/2m(V2)^2 V2 represents the second value for the velocity
K2=1/2m(V1)^2 V1 represents the first value for the velocity
U1=mgh1 h1 represents the first height, the initial height
U2=mgh2 h2 represent the recorded height
Acceleration = Radial Acceleration + Tangential Acceleration
Radial Acceleration = V^2/R

The Attempt at a Solution

(a)mgh1 + 1/2m(V1)^2 = mgh2 + 1/2m(V2)^2 from here the value of the mass cancels
gh1 + 1/2(V1)^2 = gh2 + 1/2(V2)^2 Point B is at the top of the loop -> h2=2R
And V1 = 0 because the car was at rest
gh1 = g2R +1/2(V2)^2
h1 = (2gR + 1/2(V2)^2)/g

(b) (This is where I have ran into trouble, unless I have already made mistake in part a)

I plug in the values R and H to the equation, and solve for V2. I come out with velocity being 31.3m/s. From here do I simply use Radial Acceleration = V^2/R and assume that the Tangential Acceleration is gravity because the car is perpendicular to the ground?

I solved for the final velocity at the bottom of the circle using the conservation of energy equation and found that value to be 37.04m/s. I also solved for the distance traveled, which is 1/4 of the circle using 1/4 * 2 * (3.14)R.

I then used Vf^2 = Vi^2 + 2a(y-yo) and got 6.3m/s^2. Would this be equivalent to tangential acceleration. And if so, I would not plug in the distance traveled on the loop but the change in height. Sorry, I'm thinking while I'm typing this up.

Thank you for any help that you can provide!

 

[Delphi51]

Welcome to PF!

In (a) you need to deal with the condition "without falling off the top".
This means it needs to be going fast enough so that the force of gravity doesn't pull it down (cause it to accelerate down more than its centripetal acceleration on the circular loop). Alternatively, you can think of gravity as providing the centripetal force - but no more than that or it falls.

We can't see your diagram until it is approved, which probably won't be tonight. An alternative is to upload it to a free photo site such as photobucket.com and post a link here. Use the IMG link if you have that option.