Right hand rule charged particle direction question

[outxbreak]

1. Two charged particles are traveling in circular orbits with the same speed in a region of uniform magnetic field that is directed into the page, as shown. The magnitude of the charge on each particle is identical but the signs of the charges are unequal. Which one of the entries in the table below is correct?

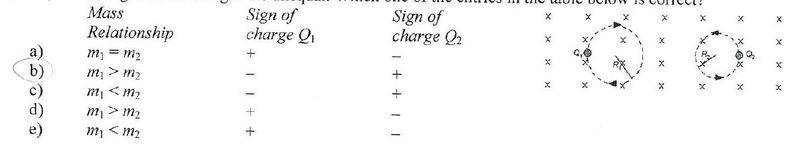
The correct answer is B

I understand that the m1>m2 just by using the formula:
r=mv/qB where I canceled the v and B and was left with
m=r*q so b.c the m1 radius is bigger it has a larger mass



2. I don't understand how to find the sign of the charge. Using the right hand rule I know that the field is going into the page but where is the velocity going or the force? I can't figure out their directions.

 

[NihalSh]

Since both particles are moving on a circular path, there must be centripetal force. This force is given by:
$$\vec{F_{m}}=q(\vec{v}\times\vec{B})$$
here $q$ is inclusive of charge. That means direction of force would also depend on sign of charge. You know the direction of every quantity, the sign of charge which is consistent with the direction of Force would be the required sign. I hope this clears out things!

Edit: direction of force would be towards center (hence the term "centripetal") and direction of velocity is given in the diagram by arrow. Velocity is always tangential to its path and hence to the circle.

 

[outxbreak]

Hi, I don't understand how to find the direction of force..
I don't know what way to point my fingers for the velocity.

 

[NihalSh]

Hi, I don't understand how to find the direction of force..
I don't know what way to point my fingers for the velocity.

The direction of force is implicitly given, a body cannot move in circular path unless a force towards the center acts on it. You need to revise circle motion to understand why that is.

you can always pick any point on the circle. The direction of velocity is tangent of the circle and it is indicated by arrow in the diagram. Find the direction of cross product. if it points towards the center then $q$ must be positive otherwise it will be negative.

 

[Nickie]

The direction of the velocity and force can be determined by using the right hand rule. Point your thumb in the direction of the velocity (tangent to the circular orbit) and your fingers in the direction of the magnetic field (into the page). Your palm will then face in the direction of the force. If the two particles have the same speed and are traveling in the same direction, the force on both particles will be in the opposite direction due to their unequal charges. This means that the force on particle 1 will be in the opposite direction of particle 2, as shown in the table. Additionally, the sign of the charge can be determined by the direction of the force. If the force is in the same direction as the velocity, the charge is positive. If the force is in the opposite direction of the velocity, the charge is negative. In this case, since the force is in the opposite direction of the velocity for particle 1, its charge must be negative.