resurgance2001
- 197
- 9
- Homework Statement
- Please see the photo of the question below with the diagram. We have to find the coefficient of friction between the rod and plane
- Relevant Equations
- Moments, Components of forces, and friction = mu x reaction force.
My solution is on the files.
The basic approac was the take moments about A. Then find the reaction at C.
Use the reaction at C to find the friction between rod and cylinder.
I take it to mean from the question that the friction between the rod and plane is equal to the friction between the rod and cylinder.
So find reaction at A.
And then divide the friction by the reaction at A.
So my real question is do you agree with the approach or can you suggest a more elegant way of solving the problem. ?
Thanks

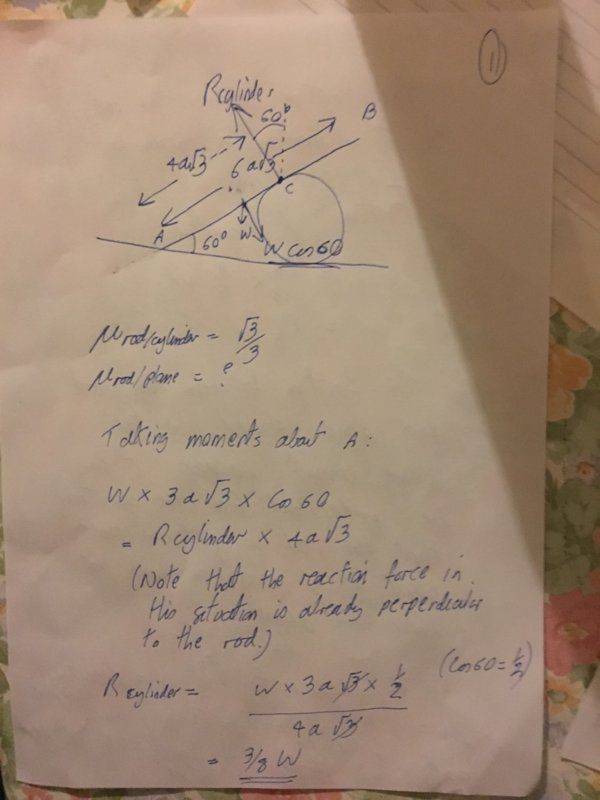
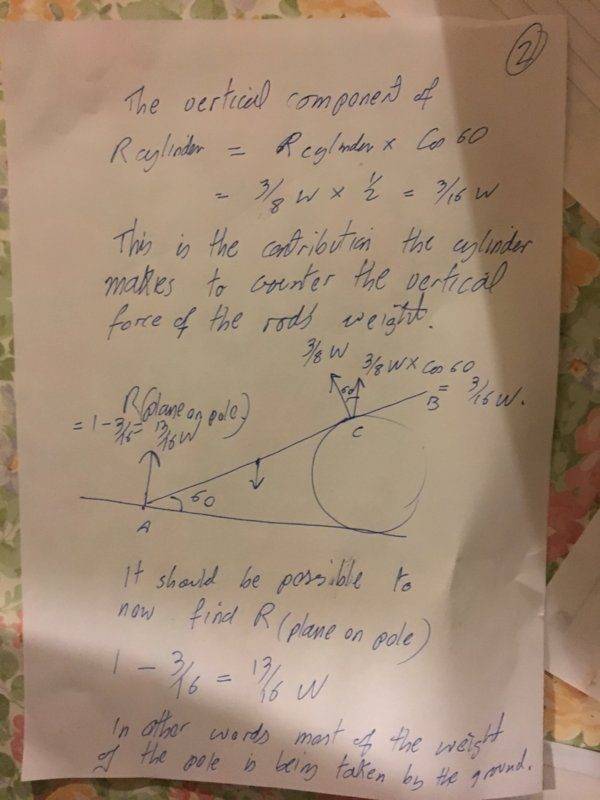


The basic approac was the take moments about A. Then find the reaction at C.
Use the reaction at C to find the friction between rod and cylinder.
I take it to mean from the question that the friction between the rod and plane is equal to the friction between the rod and cylinder.
So find reaction at A.
And then divide the friction by the reaction at A.
So my real question is do you agree with the approach or can you suggest a more elegant way of solving the problem. ?
Thanks
