Rolling Coins: Unravelling the Mystery of Two Revolutions

[agro]

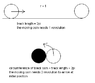
Imagine rolling a coin with a radius of 1 unit on a flat surface. To get translated 2[pi] units, the coin must obviously roll 1 revolution. (the angle swept is 2[pi] and the arc length covered equals to 2[pi]*r = 2[pi]*1 = 2[pi].

Now imagine rolling a coin on another stationary coin with the same radius (circumference = 2[pi] = length of the first track). How can it be that it requires 2 revolutions? Is it because the real track isn't the black coin but the trace of the circle's center when moving (which equals 4[pi])?

It makes me feel uneasy... Can anyone give a satisfactory/intuitive explanation?

 

[agro]

See the attached image btw...

 

[Oxymoron]

It doesn't require two revolutions, only one.

When any coin rolls along its edge on a flat surface, the distance it travels in 1 revolution is always 2*pi*r units. When you roll an coin along the edge of an identical coin, 1 revolution is still 2*pi*r units because to the coin, the surface is still flat. This means it still only takes the coin 1 revolution to roll around the other coin!

Just imagine laying out the circumference of a coin on a flat table. This length will be 2*pi*r units long. The other coin simply rolls along this = 1 revolution for the rolling coin.

If I understood your question correctly.

 

[Hurkyl]

The coin experiences one revolution because it rolled a distance of 2π radians, and the coin experiences one revolution because it was rotated 2π radians around the central coin. Add them up and you get two revolutions!

If you spun around in just the right way while doing the experiment, you'd see it experience three revolutions.

 

[HallsofIvy]

Uh, Hurkyl, this was a joke,right? (just checking)

 

[Hurkyl]

Grr, I'm thinking "rotation" while saying "revolution".

From the overhead POV, the coin undergoes two rotations through 1 revolution!