aaddcc
- 9
- 0
Hey, let's say that in 2D space we have a 2x2 rotation matrix R. Normally you could multiply this rotation matrix by a 2x1 column matrix / vector X. In that case it would be XR to get the vector rotated in the way described by R. Now what I'm wondering is, what if I had 3 column vectors that I wanted to combine and multiply column-wise. Is there a mathematical way to describe having this new matrix and doing the operation on each column individually, then putting it back into the same type of matrix?
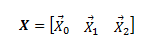 As in I want to multiply X0, X1, X2, individually by R but describe it in a simple way. I don't think I can say XR in this case... can I?
As in I want to multiply X0, X1, X2, individually by R but describe it in a simple way. I don't think I can say XR in this case... can I?