Rotation matrix multiplied by matrix of column vectors?

[aaddcc]

Hey, let's say that in 2D space we have a 2x2 rotation matrix R. Normally you could multiply this rotation matrix by a 2x1 column matrix / vector X. In that case it would be XR to get the vector rotated in the way described by R. Now what I'm wondering is, what if I had 3 column vectors that I wanted to combine and multiply column-wise. Is there a mathematical way to describe having this new matrix and doing the operation on each column individually, then putting it back into the same type of matrix?

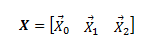As in I want to multiply X0, X1, X2, individually by R but describe it in a simple way. I don't think I can say XR in this case... can I?

 

[mathwonk]

in my notation i think you meant RX for X rotated by R. Then RZ, where Z is a matrix of any number of columns, is a matrix whose columns are the result of rotating all those columns by R.

 

[aaddcc]

Sorry, you are right I meant RX. Are you saying that if I have multiple vectors in one matrix, where each column is a vector, I can just multiply the rotation matrix by that matrix to rotate each individual vector? Or is there another way I'd need to do this?

 

[mathwonk]

i don't understand. are you asking me to repeat my statement? couldn't you just read it again?

 

[aaddcc]

Well it doesn't really make sense to me, because you are basically saying I can multiply a 2x2 matrix by a 2xn matrix which I don't think is possible for n>2? In my case I have a 2x3 matrix, i.e. 3 column vectors and a 2x2 rotation matrix

 

[mathwonk]

ok, in matrix multiplication AB you dot the rows of the left matrix A by the columns of the right matrix B. so a 2x2 matrix A can be multiplied by any matrix B with 2 rows, i.e. any 2xn matrix. do you agree?

in general, matrix multiplication is defined for any mxn matrix times any nxk matrix. i think i got this right. what do you think?