Rutherford scattering with Coulomb cutoff

[Reverend Shabazz]

Hello, I am reading a section in Jackson discussing classical Rutherford scattering, and he mentions incorporating a cutoff in the Coulomb interaction in order to model electric screening. I am trying to understand how he applies this, as described below.

The set up is basically the classic Rutherford scattering set up with charges $ze$ and $Ze$ interacting with a small angle of deflection (i.e $sin(\theta/2) \approx \theta/2$), leading to a differential scattering cross section of:

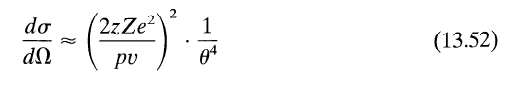
Now at $\theta=0$ of course the cross section is infinite, so he suggests modifying the Coulomb force interaction so as to drop off suddenly at $r=a$:

So I am trying to understand how he obtains eq. 13.53...or at the very least what the set up is.

My guess is that he starts with a massive incident particle approaching a less massive target particle located at the origin. The massive incident particle is assumed to remain in a straight line, while the target particle deflects. But unlike the typical straight line approximation for this scenario, the typical Coulomb interaction remains the same only within a sphere of radius $r=a$ centered either on the origin or on the particle, beyond which the force is 0. Does this sound right?

Unfortunately, I couldn't find much on the internet pertaining to this question except for an article that I don't have access to: https://aapt.scitation.org/doi/10.1119/1.1987568

 

[Vanadium 50]

I don't think he's doing anything more sophisticated than picking a functional form that behaves the way he wants: \theta^4 \rightarrow (\theta^2 + \theta_0^2)^2 has the right large-angle and small-angle behavior.

 

[Reverend Shabazz]

I don't think he's doing anything more sophisticated than picking a functional form that behaves the way he wants: \theta^4 \rightarrow (\theta^2 + \theta_0^2)^2 has the right large-angle and small-angle behavior.

I thought so too, but I have doubt since he prefaces that formula by saying:

or, in an older version of his book:

The wording sounds like he's doing more than approximating $\theta$. But I could be wrong..

For the record, the question with solution for 13.1 is found here: http://www-personal.umich.edu/~pran/jackson/P506/hw11a.pdf
It is just the simple scenario where the incident particle remains on a straight line trajectory and the Coulomb potential has no cutoff. As such, the only momentum transferred is perpendicular to the incident's velocity (see section 1.1 here for details: http://www.phys.lsu.edu/~jarrell/COURSES/ELECTRODYNAMICS/Chap13/chap13.pdf).

In the cutoff case, though, my thought is that the momentum transferred to the target in the direction parallel to the velocity will be non_zero in contrast to the no-cutoff case, and thus, when combined with the perpendicular momentum, will scatter the target at an angle. I would anticipate that, in calculating the resulting differential cross section, it would produce Jackson's result. Admittedly, I haven't tried slugging through the calculation yet.