- #1
Ravrage
- 13
- 0
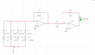
Homework Statement
Homework Equations
See above in the question
The Attempt at a Solution
I know that I need to be using a summing amp with the sinusoidal terms but I am struggling to calculate the input values that I need, also I think I need a capacitor in place of R6 but I'm not entirely sure. Any help is much appreciated :)