Scale height ##z_0## of atmosphere's density profile

[brotherbobby]

Homework Statement

A clever student has found that the density profile of the earth atmosphere is $\rho=\rho_0 \exp(-z/z_0)$, where $z$ is the height above sea level and $\rho_0$ is the density at sea level ($1.28\; \text{kg/m}^3$). If $z_0$ is the $\text{scale height}$ of the atmosphere, determine its value.

Relevant Equations

The pressure at a point in a fluid $P = \frac{dF}{dA}$ where $dF$ is the infinitesimal force exerted by the fluid on an element of area $dA$, irrespective on how it is aligned.

I want to begin by writing the problem and drawing its sketch to make things clearer on what is being asked for.

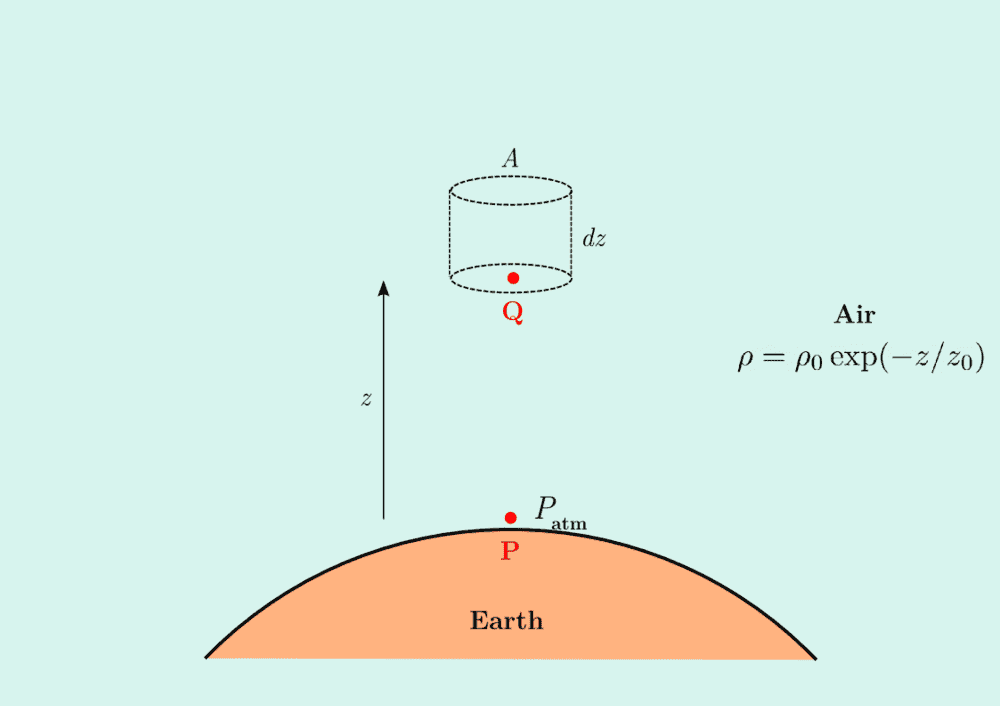Given : In the sketch shown to the right, the density profile of air with increasing $z$ is given by $\rho=\rho_0 \exp(-z/z_0)$. Since we know the value of atmospheric pressure at sea level (say at a point P) $\left( P_{\text{atm}} = 1.013\times 10^5\; \text{Pascal}\right)$, we can use it to find the value of $\mathbf{z_0}$, the scale height of the atmosphere.

Note : For decreasing air density with height, $z_0 > 0$.

Attempt : Let us imagine a capsule of air of cross section area $A$ and thickness $dz$ located at a height $z$ above the Earth surface. The infinitesimal pressure at Q due to this $dP = \frac{dF}{A} = \frac{dw}{A}= \frac{g dm}{A} = \frac{g \rho(z) d\tau}{A} = \rho(z) g dz$ (well known!).

Integrating, remembering that $P(z=\infty) = 0$ and $P(z=0) = P_{\text{atm}}$, we have : $$\int_0^{P_{\text{atm}}} dP = g \rho_0 \int_{\infty}^0 e^{-z/z_0} dz \Rightarrow P_{\text{atm}} = -\rho_0 g z_0\;\; \cancelto{1}{\left[e^{-z/z_0}\right]_{\infty}^0}$$

This leads to $$z_0 = \frac{P_{\text{atm}}}{-\rho_0 g} = \frac{-1.013\times 10^5}{1.28 \times 9.8} = \boxed{-8.07 \times 10^3\; \text{m}}$$.

Answer : The answer from the book is the same, but positive (as it should be!) $\boxed{z_0 = 8.1\times 10^3\; \text{m} }$.

Where am I mistaken?

 

[BvU]

$$dP = \frac{dF}{A} = \frac{dw}{A}= \frac{g dm}{A} = \frac{g \rho(z) d\tau}{A} = \rho(z) g dz$$
(well known!).

I only know it well with a minus sign ...

The infinitesimal pressure at Q

you mean the infinitesimal pressure difference $P(z) - P(z+dz)$ which is positive, but it is $-dP$

 

[brotherbobby]

I only know it well with a minus sign ...

Thank you. Yes, I remember that $\frac{dP}{dz} = -\rho g$ if $z$ is pointing up. Pressure in a fluid increases with depth, but decreases with height. I suppose I should have done the same as books do to derive the differential equation above : match forces above and below the elemental area.

Solved.