foxdiligens
- 1
- 0
- TL;DR
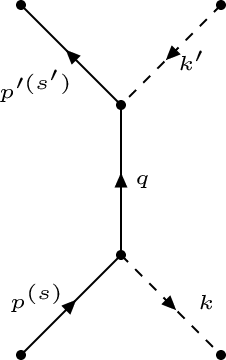
- Feynman diagrams at tree level contributing to the scattering of a fermion and a scalar particle.
Hello everyone,
I am working on the following problem: I would like to determine the invariant Matrix element of the process ##\psi\left(p,s\right)+\phi\left(k\right)\rightarrow\psi\left(p',s'\right)+\phi\left(k'\right)## within Yukawa theory, where ##\psi\left(p,s\right)## denotes a fermion with momentum p and spin s and ##\phi\left(k\right)## denotes a real scalar particle with momentum k. The Lagrangian is given by:
##\mathcal{L}=\overline{\psi}\left(i\gamma^\mu\partial_\mu-M\right)\psi+\frac{1}{2}\left(\partial_\mu\phi\right)\left(\partial^\mu\phi\right)-\frac{m}{2}\phi^2-g\overline{\psi}\psi\phi##
Which Feynman diagrams contribute on tree level and how are they translated into the invariant matrix element? Following my considerations, this is the s-channel only, which is represented by this diagram:
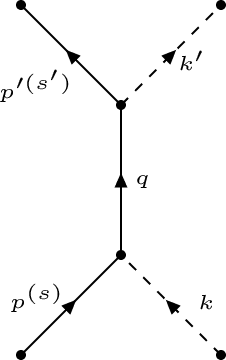
I would write the matrix element as follows:
##i\mathcal{T}=\int\frac{dq^4}{\left(2\pi\right)^4}\overline{u}_{s'}\left(p'\right)\left(-ig\right)\left(2\pi\right)^4\delta^{(4)}\left(q-p'-k'\right)\frac{i\left(\gamma^\mu q_\mu+M\right)}{q^2-M^2}\left(-ig\left(2\pi\right)^4\delta^{\left(4\right)}\left(p+k-q\right)\right)u_s\left(p\right)##
which yields this invariant matrix element:
##\mathcal{M}=-\frac{g^2}{s+M^2}\overline{u}_{s'}\left(p'\right)\left(\gamma^\mu q_\mu+M\right)u_s\left(p\right).##
I utilized the following Feyman rules:
I hope you can bring some clarity to my question. Thank you very much in advance!
I am working on the following problem: I would like to determine the invariant Matrix element of the process ##\psi\left(p,s\right)+\phi\left(k\right)\rightarrow\psi\left(p',s'\right)+\phi\left(k'\right)## within Yukawa theory, where ##\psi\left(p,s\right)## denotes a fermion with momentum p and spin s and ##\phi\left(k\right)## denotes a real scalar particle with momentum k. The Lagrangian is given by:
##\mathcal{L}=\overline{\psi}\left(i\gamma^\mu\partial_\mu-M\right)\psi+\frac{1}{2}\left(\partial_\mu\phi\right)\left(\partial^\mu\phi\right)-\frac{m}{2}\phi^2-g\overline{\psi}\psi\phi##
Which Feynman diagrams contribute on tree level and how are they translated into the invariant matrix element? Following my considerations, this is the s-channel only, which is represented by this diagram:
I would write the matrix element as follows:
##i\mathcal{T}=\int\frac{dq^4}{\left(2\pi\right)^4}\overline{u}_{s'}\left(p'\right)\left(-ig\right)\left(2\pi\right)^4\delta^{(4)}\left(q-p'-k'\right)\frac{i\left(\gamma^\mu q_\mu+M\right)}{q^2-M^2}\left(-ig\left(2\pi\right)^4\delta^{\left(4\right)}\left(p+k-q\right)\right)u_s\left(p\right)##
which yields this invariant matrix element:
##\mathcal{M}=-\frac{g^2}{s+M^2}\overline{u}_{s'}\left(p'\right)\left(\gamma^\mu q_\mu+M\right)u_s\left(p\right).##
I utilized the following Feyman rules:
- Fermionic propagator: ##\frac{i\left(\gamma^\mu q_\mu+M\right)}{q^2+M^2}##
- Vertex: ##-ig##
- Incoming/outgoing external fermion: ##u_s\left(p\right)/\overline{u}_{s}\left(p\right)##
- External boson, incoming or outgoing: ##1##
I hope you can bring some clarity to my question. Thank you very much in advance!