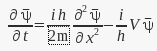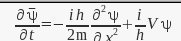SUMMARY
The discussion focuses on the application of the complex conjugate in the Schrödinger equation (S.E) and the implications of conjugating the wave function ψ. It clarifies that the derivative with respect to time, when expressed in terms of the complex conjugate ψ*, remains valid as long as the original equation is valid. Key c-number conjugation rules are highlighted, including the conjugation of products and sums, as well as the derivative of the wave function. The importance of the product rule in this context is emphasized, aiding in the understanding of the equation's transformation.
PREREQUISITES
- Understanding of the Schrödinger equation in quantum mechanics
- Familiarity with complex numbers and their properties
- Knowledge of calculus, specifically derivatives and the product rule
- Basic grasp of wave functions in quantum physics
NEXT STEPS
- Study the derivation and implications of the Schrödinger equation in quantum mechanics
- Learn about complex conjugates and their role in quantum mechanics
- Explore the product rule in calculus and its applications in physics
- Investigate the significance of wave functions and their transformations in quantum theory
USEFUL FOR
Students of quantum mechanics, physicists, and anyone interested in the mathematical foundations of the Schrödinger equation and its applications in quantum theory.