- #1
Yukterez
- 85
- 14
The Schwarzschild equation of motion, where coordinate length is differentiated by proper time is as far as I know
[tex]r''(t) = -\frac{G\cdot M}{r(t)^2} + r(t)\cdot{\theta}'(t)^2 - \frac{3\cdot G\cdot M\cdot{\theta}'(t)^2}{c^2}[/tex]
[tex]{\theta}''(t) = -2\cdot r'(t)/r(t)\cdot{\theta}'(t)[/tex]
Now the question is, how do I choose my initial conditions for the angular and the radial initial velocities, for example, if I want to test the orbit of a test particle close to the speed of light [itex]v_0=0.999c[/itex] at the photon sphere [itex]r_0=1.5r_s[/itex]?
I am not sure if my approach is correct, but when I try
[tex]\dot{\theta}_0\cdot r_0 = \frac{\xi_0}{ \color{red}{\sqrt{ 1-v_0^2/c^2}}\cdot \color{blue}{\sqrt{1-r_s/r_0}}}[/tex]
with [itex]\xi_0[/itex] as the transversal component of [itex]v_0[/itex] and [itex]\kappa_0[/itex] as the radial component:
[tex]\dot{r}_0\ = \frac{\kappa_0\cdot \color{blue}{\sqrt{1-r_s/r_0}}}{ \color{red}{\sqrt{ 1-v_0^2/c^2}}}[/tex]
so that [itex]\xi = cos(\varphi_0), \kappa = sin(\varphi_0)[/itex] with [itex]\varphi[/itex] as the launching angle from the shell, the orbits look like I would expect them, at least in the transversal direction:
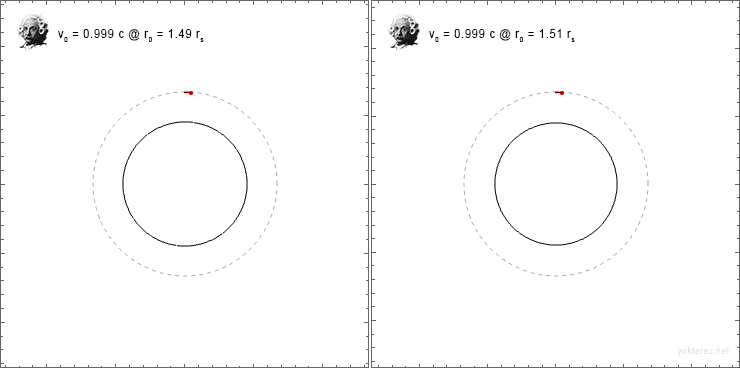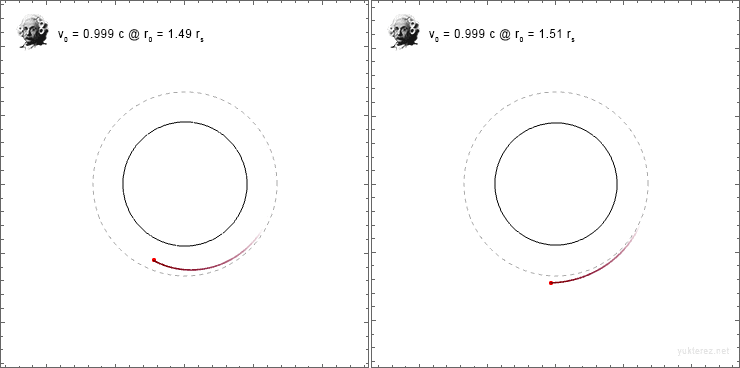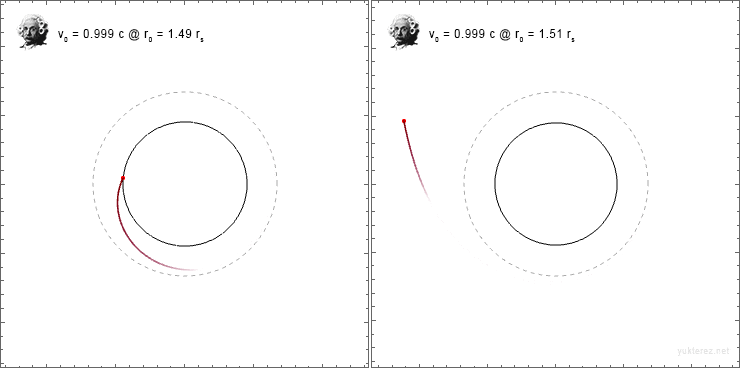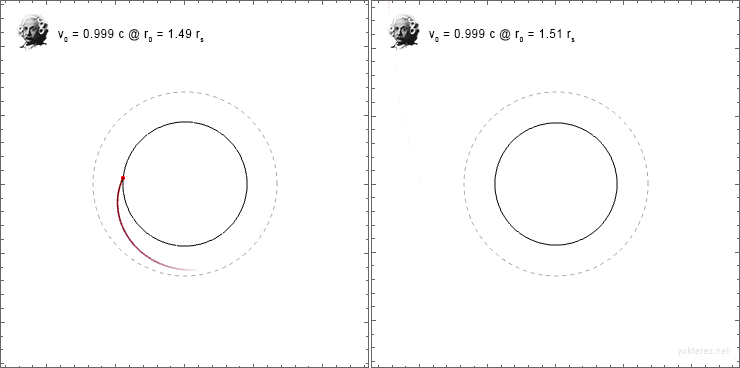
But since radial and transverse directions have the factor [itex]\color{blue}{\sqrt{1-r_s/r_0}}[/itex] on different sides of the fraction, the inital angle is not conserved.
So are my initial conditions even correct, and if not, how would one transform the radial and the transversal components of the initial velocity [itex]v_0[/itex] to [itex]\dot{r}(0)[/itex] and [itex]\dot{\varphi}(0)[/itex]?
_____________________________________________________
If it is of interest, the code for the plot is in Mathematica Syntax
[tex]r''(t) = -\frac{G\cdot M}{r(t)^2} + r(t)\cdot{\theta}'(t)^2 - \frac{3\cdot G\cdot M\cdot{\theta}'(t)^2}{c^2}[/tex]
[tex]{\theta}''(t) = -2\cdot r'(t)/r(t)\cdot{\theta}'(t)[/tex]
Now the question is, how do I choose my initial conditions for the angular and the radial initial velocities, for example, if I want to test the orbit of a test particle close to the speed of light [itex]v_0=0.999c[/itex] at the photon sphere [itex]r_0=1.5r_s[/itex]?
I am not sure if my approach is correct, but when I try
[tex]\dot{\theta}_0\cdot r_0 = \frac{\xi_0}{ \color{red}{\sqrt{ 1-v_0^2/c^2}}\cdot \color{blue}{\sqrt{1-r_s/r_0}}}[/tex]
with [itex]\xi_0[/itex] as the transversal component of [itex]v_0[/itex] and [itex]\kappa_0[/itex] as the radial component:
[tex]\dot{r}_0\ = \frac{\kappa_0\cdot \color{blue}{\sqrt{1-r_s/r_0}}}{ \color{red}{\sqrt{ 1-v_0^2/c^2}}}[/tex]
so that [itex]\xi = cos(\varphi_0), \kappa = sin(\varphi_0)[/itex] with [itex]\varphi[/itex] as the launching angle from the shell, the orbits look like I would expect them, at least in the transversal direction:
But since radial and transverse directions have the factor [itex]\color{blue}{\sqrt{1-r_s/r_0}}[/itex] on different sides of the fraction, the inital angle is not conserved.
So are my initial conditions even correct, and if not, how would one transform the radial and the transversal components of the initial velocity [itex]v_0[/itex] to [itex]\dot{r}(0)[/itex] and [itex]\dot{\varphi}(0)[/itex]?
_____________________________________________________
If it is of interest, the code for the plot is in Mathematica Syntax
Code:
G = 1; M = 1; c = 1; rs = 2 G M/c^2; T = tMax G M/c^3;
r0 = 151/100 rs; vo = 999/1000 c; φ = Pi/2; θ0 = 0; tMax = 2;
vr0 = vo Cos[φ]/j*k; vθ0 = vo/r0 Sin[φ]/j/k;
d1 = T/10; d2 = d1; wp = 30; step = T/200;
j = Sqrt[1 - vo^2/c^2];
k = Sqrt[1 - rs/r0];
sol = NDSolve[{
r''[t] == -((G M)/r[t]^2) + r[t] θ'[t]^2 - (3 G M)/c^2 θ'[t]^2,
r'[0] == vr0,
r[0] == r0,
θ''[t] == -((2 r'[t] θ'[t])/r[t]),
θ'[0] == vθ0,
θ[0] == θ0,
τ'[t] == Sqrt[c^2 r[t] + r[t] r'[t]^2 - c^2 rs + r[t]^3 θ'[t]^2 - r[t]^2 rs θ'[t]^2]/(c Sqrt[r[t] - rs] Sqrt[1 - rs/r[t]]),
τ[0] == 0
}, {r, θ, τ}, {t, 0, T}, WorkingPrecision -> wp,
MaxSteps -> Infinity, Method -> Automatic,
InterpolationOrder -> All];
t[ξ_] :=
Quiet[χ /.
FindRoot[
Evaluate[τ[χ] /. sol][[1]] - ξ, {χ, 0},
WorkingPrecision -> wp, Method -> Automatic]];
Τ := Quiet[t[ι]];
x[t_] := (Sin[Evaluate[θ[t] /. sol]] Evaluate[r[t] /. sol])[[1]]
y[t_] := (Cos[Evaluate[θ[t] /. sol]] Evaluate[r[t] /. sol])[[1]]
s[text_] := Style[text, FontSize -> font]; font = 11;
(* Eigenzeit, Celerity *) Do[Print[
Rasterize[Grid[{{Show[Graphics[{
{Black, Circle[{0, 0}, rs]},
{Lighter[Gray], Dashed, Circle[{0, 0}, r0]}},
Frame -> True, ImageSize -> 400, PlotRange -> 2 r0],
Graphics[{PointSize[0.01], Red, Point[{x[т], y[т]}]}],
ParametricPlot[{x[η], y[η]}, {η, 0, т},
ColorFunction -> Function[{x, y, η},
Hue[0.85, 1, 0.5, Max[Min[(-т + (η + d1))/d1, 1], 0]]],
ColorFunctionScaling -> False],
ParametricPlot[{x[η], y[η]}, {η, 0, т},
ColorFunction -> Function[{x, y, η},
Hue[0, 1, 0.5, Max[Min[(-т + (η + d2))/d2, 1], 0]]],
ColorFunctionScaling -> False]]},
{Grid[{
{" ", s["proper time"], " = ", s[N[т, 8]], s["GM/c³"]},
{" ", s["coordinate time"], " = ", s[N[Evaluate[τ[т] /. sol][[1]], 8]], s["GM/c³"]},
{" ", s["time dilation"], " = ", s[N[Evaluate[τ'[т] /. sol][[1]], 8]], s["dτ/dt"]},
{" ", s["angle"], " = ", s[N[Evaluate[(θ[т] /. sol) 180/Pi][[1]], 8]], s["grad"]},
{" ", s["radial distance"], " = ", s[N[Evaluate[r[т] /. sol][[1]], 8]], s["GM/c²"]},
{" ", s["x-Axis"], " = ", s[N[x[т], 8]], s["GM/c²"]},
{" ", s["y-Axis"], " = ", s[N[y[т], 8]], s["GM/c²"]}
}, Alignment -> Left]}}, Alignment -> Left]]
], {т, step, T, step}]