SUMMARY
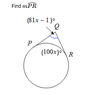
The discussion focuses on calculating arc lengths in circles using secant and tangent angles. The angles $$\angle CPQ$$ and $$\angle CRQ$$ are established as both being 90 degrees due to the tangents $$\overline{QP}$$ and $$\overline{QR}$$. The equation derived from the sum of the interior angles of a quadrilateral leads to the conclusion that the measure of the arc $$\overset{\frown}{PR}$$ is 100 degrees. This calculation is crucial for accurately determining arc lengths in circle geometry.
PREREQUISITES
- Understanding of circle geometry, specifically secant and tangent properties.
- Familiarity with angle relationships in quadrilaterals.
- Basic algebra skills for solving equations.
- Knowledge of arc measures and their calculations.
NEXT STEPS
- Study the properties of tangents and secants in circle geometry.
- Learn how to calculate arc lengths using central angles.
- Explore the relationship between inscribed angles and intercepted arcs.
- Practice solving problems involving quadrilaterals inscribed in circles.
USEFUL FOR
Students studying geometry, educators teaching circle properties, and anyone looking to enhance their understanding of arc length calculations in circles.