Semicircular ring falling through a Magnetic Field

[zorro]

Homework Statement

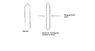
A thin semicircular conducting ring of radius R is falling with its plane vertical in a horizontal magnetic field B (see fig). At the position MNQ, speed of the ring is v and the potential difference developed across the ring is - (options are given)

The Attempt at a Solution

First of all, I am not sure whether we can find the flux throug the semi-circle because it does not form a closed loop.

Assuming we can find it out ,
Φ = BπR²/2

The rate of change of magnetic flux is 0 (RHS is constant)
Hence the e.m.f. induced is 0.

The answer doesnot match :|

 

[collinsmark]

First of all, I am not sure whether we can find the flux throug the semi-circle because it does not form a closed loop.

That just means that there won't be a current flowing through the conductor. But there can still be an induced emf.

Assuming we can find it out ,
Φ = BπR²/2

Looks okay to me so far, for the instant that the semicircular ring is at position position MNQ

The rate of change of magnetic flux is 0 (RHS is constant)
Hence the e.m.f. induced is 0.

Don't jump to conclusions! I agree that the rate of change of the magnetic field is zero, but is that also true for the flux?

By definition,

Φ = BA​

and

ε = -dΦ/dt​

thus,

ε = -d(BA)/dt.​

We know that B is a constant, but what about the area A? At the moment the semicircular loop passes through position MNQ and after, does the area defined by the section of the hoop that happens to be within the magnetic field change with time?

 

[zorro]

We know that B is a constant, but what about the area A? At the moment the semicircular loop passes through position MNQ and after, does the area defined by the section of the hoop that happens to be within the magnetic field change with time?

Just before the semi-ring reaches the position MNQ, there is no change in the area it encloses. So there should not be any E.M.F.
E.M.F is induced only after it starts passing through this position.

 

[Dadface]

Hello Abdul,E=-BdA/dt but B is constant so you are trying to find dA/dt which is the area swept out in one second.Try extending your sketch as follows:
1. Draw the semicircle as you did above.
2. Draw the semicircle again but after it has moved to a lower position.
3. Shade in the area swept out by the semicircle.

From this you should be able to see what the area would be for one second and a velocity v.
(assume that the semicircle remains in the field,the situation is different as it enters and emerges)

 

[zorro]

Hello Abdul,E=-BdA/dt but B is constant so you are trying to find dA/dt which is the area swept out in one second.Try extending your sketch as follows:
1. Draw the semicircle as you did above.
2. Draw the semicircle again but after it has moved to a lower position.
3. Shade in the area swept out by the semicircle.

From this you should be able to see what the area would be for one second and a velocity v.
(assume that the semicircle remains in the field,the situation is different as it enters and emerges)

See the attached figure.
What do I deduce from the area swept? I think finding out that area as a function of time is tedious.

 

[Dadface]

Abdul,I think it is only the horizontal elements of the wire that cut the field.The problem is equivalent to a straight wire of length equal to 2r moving with velocity v.Look at your diagram and draw two diameters one for the wire in the top position and two for the wire in the bottom position.From this can you see a non tedious way of finding the area?

 

[zorro]

Do you mean that area swept by the diameter equals the area swept by the ring in a fixed time?

 

[Dadface]

Have a look.Subtract the area above the top diameter and add this to the area above the bottom diameter.How,if at all,does the area swept out by the diameter differ from the area you shaded?

 

[zorro]

Oh yes - the areas swept are same.
So the induced EMF is E=2BRv
Last question - which point is at a higher potential - M or Q?

 

[collinsmark]

Oh yes - the areas swept are same.
So the induced EMF is E=2BRv

'Looks good to me. That's what I got for the situation where the entire semicircular piece of wire is in the field.

Last question - which point is at a higher potential - M or Q?

Recall,

F = qv x B.​

Now imagine that wire contains some positive charges on it (which it actually does. It also contains an equal amount of negative charges too, but let's just consider the positive charges for the moment).

Using the right-hand-rule (or whatever applicable rule you wish to use for the cross product), which direction would these positive charges be "pushed"?

Now, hypothetically, if you were to take the wire out of the magnetic field and attach it to the terminals of a battery, what polarity would use such that the current flows in the same direction as those positive charges were previously "pushed"?

(Now if you were curious and wanted to consider the negative charges too, they will be forced in the opposite direction that the positive charges were, in the situation where the wire is moving in the magnetic field. And when taken out of the field and connected to the battery, the "current" flows in the opposite direction as the negative charges, so the answer still comes out to be the same as before.)

 

[zorro]

The positive charges will be pushed towards right. So Q is at a higher potential.
Thanks a lot!

 

[collinsmark]

The positive charges will be pushed towards right. So Q is at a higher potential.
Thanks a lot!

Wait, hold on.

I agree that the positive charges would be pushed toward the right. .

But if you took the wire out of the magnetic field, attached it to a battery such that the battery's positive terminal was on Q and the negative terminal on M, the current (thus positive charges) would flow through the wire to the left.

So you should re-think that last part.

[Edit: If you'd like to think about it another way, the positive side of the induced emf is going to push the positive charges in the wire away from it. Which side of the wire are the positive charges being pushed away from?]

 

[zorro]

Wait, hold on.

I agree that the positive charges would be pushed toward the right. .

But if you took the wire out of the magnetic field, attached it to a battery such that the battery's positive terminal was on Q and the negative terminal on M, the current (thus positive charges) would flow through the wire to the left.

So you should re-think that last part.

The ring doesnot form a closed loop. So you cannot hypothetically take the wire out of the magnetic field and attach it to a battery as that is applicable only in the case of closed loops .

 

[zorro]

I thought about one more possibility while thinking about the problem.
What will be the e.m.f induced int the semi-ring if the velocity is parallel to the diameter?
Will it be same as above - 2BRv ?

 

[Dadface]

Try it out,use the same method as before.

 

[zorro]

I am confused - in this case the area swept by the diameter is 0 whereas it is not so for the semi-ring.

 

[Dadface]

In the original case there was an area swept out by the horizontal elements of the wire and zero area swept out by the vertical elements the system being equivalent to a horizontal wire of length equal to the diameter.In this new case the area will be swept out by vertical elements of the wire and,as you noticed,zero area swept out by the horizontal elements.Draw a sketch as you did before and you should be able to see it.

 

[zorro]

There are no significant vertical elements - only at the ends on the wire. So I think the area swept by them will be negligible and e.m.f induced is 0. Is it fine?

 

[Dadface]

There are no significant vertical elements - only at the ends on the wire. So I think the area swept by them will be negligible and e.m.f induced is 0. Is it fine?

No,an emf will be induced.Each tiny element of wire can be considered to have a horizontal and a vertical component being vertical only at the two ends and horizontal only in the middle.The effective sum of the horizontal lengths of all the elements=2r,what is the effective sum of the vertical lengths?

 

[zorro]

Is it πR ?

 

[Dadface]

The vertical distance between the two ends and the top of the semicircle(the height)=r.Have another look at your original diagram.

 

[zorro]

ok. Is the emf induced = Brv ?

 

[Dadface]

Yes.

 

[zorro]

I spent last 30 minutes thinking about this problem
After a careful analysis, it seems that I don't agree with your previous answer.

According to me the e.m.f. induced should be 0 in this case. Here is my explanation -
If you consider a quarter of the semi-circle (say left one), then you will find out that the vertical projection of this quarter along y-axis is towards + y-axis (upwards). You can resolve this into a vertical conductor of length r. E.M.F produced is Brv.
Now if you consider the next quarter, its vertical projection is directed along - y axis. E.M.F. produced is - Brv.
So the e.m.f s induced across these two quarters cancel each other. Hence the e.m.f. induced is 0.

If you take a look at the previous question, each quarter has the horizontal projection towards the positive x-axis. So the e.m.f. due to each projection gets added up.

I hope I am correct.

 

[Dadface]

In your question the ring was moving parallel to the diameter,in other words both quarters were moving in the same x direction.Imagine bringing the two ends together so they touched and then straightening the whole thing so that in effect you have a single vertical wire made of two equal length vertical wires in contact.There is no cancelling,the emf across the whole thing being the same in size and direction as the emf across each half when considered separately.Of course the length will now be pi*r.

 

[zorro]

In your analogy, you are actually stretching the semi-ring into a straight wire of length πR and finding the e.m.f. (indirectly though)
But that is not correct as there will be a small bend in between and the direction of movement of charged particles (whether negative or positive) is reversed. Consider the left wire (in your case), the lorentz force on a positively charged particle is upwards. It is again upwards in the right wire. Assume that the positively charged particles form a continuous tube. These two opposing forces cancel each other. So there is no movement of charged particles. Hence e.m.f. induced is 0 again.

 

[Dadface]

In my analogy if the two sides make contact along their length then the whole thing can be considered as a thicker single wire.It is the movement of charged particles(electrons)along the wire/ring that causes a negative charge to build up at one end with a resulting equal positive charge at the other and this is what actually causes the emf to be developed.Equilibrium is reached when the repulsive force per electron due to the charge build up becomes equal to the Lorentz force this being when e=Blv(l being equivalent length of structure)

 

[zorro]

If you consider the semi-ring to be a thick wire, then you are changing the question i.e. you are forming a closed loop ( by merging the open ends into one wire ). You can do something else - keep the wire insulated electrically and bring them close enough. Then apply what I told in my previous post. Refer the figure -

The distance between each wire is very very small. It is magnified for a clear view.

 

[Dadface]

In your previous post you gave the example of the force on positive charges being upwards in both the left and right wire.Well,the force on like charged particles is indeed in the same direction for both wires,or in all sections of a single wire or whatever arrangement is used.It is only some electrons that are free to move and it is because the force is in the same direction for particles of like charge that an emf is induced in the first place so I don't understand your point.Are you saying that there are two forces in the same direction which cancel each other out.Anyway, its 12 ocklock here and time for bed.

 

[zorro]

Well I just modeled it that way to prove your point wrong. I assumed all the positively charged particles to form a continuous incompressible stream. There is a pushing force acting on each end of the vertical wires. If the stream of electrons in the left wire gets pushed upwards, the force in the right wire pushes it upwards to cancel the motion. Refer figure -

You can also consider it this way - the left end of the wire forms a positive terminal of an imaginary battery . Similarly the right end forms a positive terminal resulting in opposition of batteries and cancelling of e.m.f.

There can be some flaws in this explanation. I just modeled it my way.
But I still base my confident explanation in post number 24.