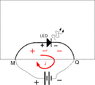collinsmark
Science Advisor
Homework Helper
- 3,445
- 3,541
You can do anything you want to hypothetically, hypothetically speaking.Abdul Quadeer said:collinsmark said:Wait, hold on.
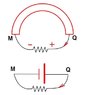
I agree that the positive charges would be pushed toward the right..
But if you took the wire out of the magnetic field, attached it to a battery such that the battery's positive terminal was on Q and the negative terminal on M, the current (thus positive charges) would flow through the wire to the left.
So you should re-think that last part.
[Edit: If you'd like to think about it another way, the positive side of the induced emf is going to push the positive charges in the wire away from it. Which side of the wire are the positive charges being pushed away from?]
The ring doesnot form a closed loop. So you cannot hypothetically take the wire out of the magnetic field and attach it to a battery as that is applicable only in the case of closed loops.
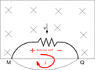
What I was attempting to do was illustrate an important point. There is an emf induced on the semicircle, even if it is isn't a closed loop. Just like a battery will have a positive and negative terminals on it, even if it doesn't happen to be connected to anything at a particular time.
It's not valid to state, "a battery, standing by itself, does not have positive or negative terminals because its not conducting current." The truth is that it has an emf across the terminals, and it also has a polarity, whether it is conducing current or not.
And one method to determine the battery's polarity is to determine which direction the current would flow when connected in a closed loop, even if that process is done hypothetically.
Here, the wire is not analogous to the battery itself. But the wire will have an emf induced across it as if a battery was connected to it, even if there is no current. If you had a voltmeter connected to the moving wire, you could measure this induced emf.
You and Dadface have discussed this already to some extent, but I think there is some confusion that I want to clear up.I thought about one more possibility while thinking about the problem.
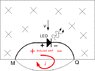
What will be the e.m.f induced int the semi-ring if the velocity is parallel to the diameter?
Will it be same as above - 2BRv ?
There is an induced emf across the wire, in this second situation (where the wire moves to the side instead of down). But it's not induced between points M and Q. The potential between points M and Q is zero. But there is an non-zero induced emf between points N and M, which is the same emf induced between points N and Q. And as you have already calculated, the value of the emf is Brv. I just wanted to make sure we're all on the same page there. I'll leave it up to you to determine the polarity of the emf.