Series RLC Circuit Response: Finding Natural and Forced Responses

[juicev80]

Homework Statement

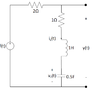
I attached a picture of the circuit.

f(t) = (e^-t)u(t), V_C(0^-) = 2V, i_L(0^-) = 1A

Obtain an expression for the total response, y(t), for the given system by finding
the natural and the forced responses.

Homework Equations

v(t) = Ri(t)
v(t) = Ldi(t)/dt
v(t) = (1/C)∫i(t)dt

The Attempt at a Solution

Ok, the first thing I did was combine the two series resistors. What I am thinking is that I will solve for the response of i(t) and then sub that into the formula f(t) - R_2Ω*i(t) = y(t). I feel like there should be a way to solve for the voltage y(t) directly, but I haven't been able to figure out how to setup the equation.

So, solving for the response of i(t) I do KVL and get 3i(t) + di(t)/dt + 2\inti(t)dt = f(t), taking this equation and differentiating it, I get: d² i(t)/dt² + 3di(t)/dt + 2i(t) = -e^-tu(t). The general form of the equation will be i(t) = i_n(t) + i_f(t). Solving for the natural response first: d² i(t)/dt² + 3di(t)/dt + 2i(t) = 0, Δ(s) = s² + 3s + 2 = 0 = (s+1)(s+2) so, i_n(t) = Ae^-t + Be^-2t for t>0.

So, at this point I need to solve for the forced response using the original equation I found, I don't know exactly how to do that: d² i(t)/dt² + 3di(t)/dt + 2i(t) = -e^-tu(t).


I have two questions: #1 is it possible to write a differential equation right off the bat which includes y(t)? questions#2 If i am on the right track so far with the above, what is the next step in finding the forced response?

P.S. I know there are much easier ways of solving this but the problem requires that I solve it using this method...

 

[rude man]

First thing is you assign symbols to the components. So you have R1, R2, L and C. Let R1 = 1 ohm.
Now, write your equation for i(t).

Since it's a 2nd order system you need two initial conditions. What is the initial voltage on C? (This has to be given to you in the problem, I'm not asking you to figure it out).