Show that ##\sin(\arctan x) < x < \tan(\arcsin x)##

[Rectifier]

The problem
For $0 < x < 1$ . Show that
$$ \sin(\arctan x) < x < \tan(\arcsin x) $$

The attempt
I know that $\sin x < x < \tan x$ is true for $0 < x < \ \pi / 2$

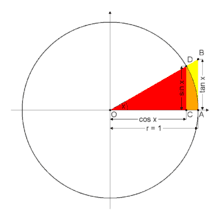x - is by definition the length DA (in radians)

I draw a right triangle with sides x and 1 and with hypotenuse $\sqrt{x^2+1}$

$\sin v = \frac{x}{\sqrt{x^2+1}}$

$\tan v = \frac{x}{1} \Rightarrow v = \arctan \ x$

$\sin (\arctan \ x) = \frac{x}{\sqrt{x^2+1}}$I am trying to write an expression for $\tan(\arcsin(x))$

$\sin v = \frac{x}{\sqrt{x^2+1}} \Rightarrow v = \arcsin \left( \frac{x}{\sqrt{x^2+1}} \right)$

$\tan v = x \Rightarrow \tan \left( \arcsin \left( \frac{x}{\sqrt{x^2+1}} \right) \right) = x$

But I fail. Please Help me write an expression for $\tan(\arcsin(x))$.

 

[mfb]

I don't think this is necessary. You can compare arctan(x) and arcsin(x) with x.