Show the Solution to a Cartesian Oval Homework Problem

[fluidistic]

Homework Statement

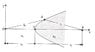
See the picture for the situation of the problem.
I'm told that any ray starting from S and getting through the "Cartesian Oval" reach point P.
I must show that the equation of the interface curve is l_0n_1+l_i n_2=K where K is a constant.
So far I've showed that l_0=\sqrt {x^2+y^2} and l_i=\sqrt {y^2+(s_0 + s_i -x)^2}. But I remain stuck as how to proceed further.
Any idea is greatly appreciated.

Homework Equations

Snell's law? I've tried something with it but didn't reach anything.
Maybe Fermat's principle?

The Attempt at a Solution

See above.

 

[rl.bhat]

Since the points S and P are fixed, the total time taken by the light to travel from S to P must be constant.
So t1 = l1/v1 and t2 = l2/v2
Now v1 = C/n1 and v2 = C/n2, where C is the velocity of the light in vacuum.
Hence find t = t1 + t2 = ...?

 

[fluidistic]

Since the points S and P are fixed, the total time taken by the light to travel from S to P must be constant.
So t1 = l1/v1 and t2 = l2/v2
Now v1 = C/n1 and v2 = C/n2, where C is the velocity of the light.
Hence find t = t1 + t2 = ...?

Thank you so much! Really bright and not complicated. Yet I totally missed it.
Problem solved!