Side kick on a falling object, mechanical energy and work

[Karagoz]

If an object with 1kg mass falls free (no air drag), from 100 meters high, and the gravitational acceleration is 9.81, then the mechanical energy will be: 1*9.81*100 = 981 joules.

The work the gravitational force does on the object will be: 9.81N*100m = 981 joules.

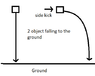
Another object with same mass (1kg) falls free from same height (100 meters) high, and gravitational acceleration is the same here too (9.81). But someone gives a horizontal kick on that object while it's falling.

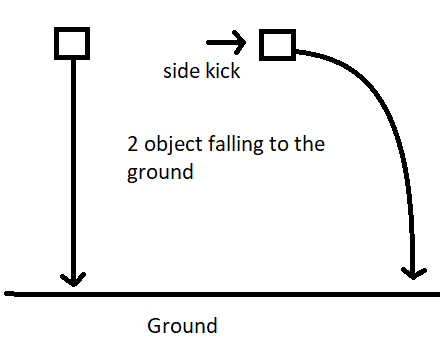
Both will fall on the ground at the same time, but the second object will have longer path since it's moved sideways. Longer path on same time means it moved faster.
Does it mean that the second object had higher kinetic energy?
Also that the side-kick gave it higher kinetic energy?

Or since the force is applied from the side, the grade between the force and the path of the object is 90 degrees. then it's:
Work = F*s*cos90 = 0?
No work done on the object means the mechanical force didn't increase or decrease. Both objects have same mechanical energy.

 

[Dylanden]

Hello

The second object had higher kinetic energy. But.
Think a little. Like Galileo. Or Einstein. He loves train...

If you let fall a stone in a train, stopped or running, the stone will fall on the floor of the train.
But if you let it fall through the window of the moving train, in addition to its speed of falling, it has the speed of the train. And she may break when she gets to the tracks.
Here.
Dylan.

 

[Dale]

Or since the force is applied from the side, the grade between the force and the path of the object is 90 degrees. then it's:
Work = F*s*cos90 = 0?

It is only 90 deg while the object is falling vertically. Once it starts moving off vertical then the horizontal force is no longer at 90 deg.

 

[pixel]

It is only 90 deg while the object is falling vertically. Once it starts moving off vertical then the horizontal force is no longer at 90 deg.

OP is asking about an kick to the side, not a continuous horizontal force.

 

[Dale]

OP is asking about an kick to the side, not a continuous horizontal force.

It doesn’t matter. To properly analyze an impulsive force you take a finite force over a finite time, and then find the limit as the time goes to zero and the force goes to infinity. All of my comments apply regardless of the duration or magnitude of the kick force.

 

[jbriggs444]

OP is asking about an kick to the side, not a continuous horizontal force.

There are a number of ways to think about the situation. @Dale's approach is the most rigorous. One might also consider that the product of an infinite force applied over a zero distance is not zero. It's indeterminate. One has to use a different calculation (such as a limit process) to obtain a meaningful result.

 

[Dylanden]

Hello
Tanks for your answers, Mr Jbriggs 444 and Mr Dale.
But Galileo explains that carefully.
If something falls from a mast of a sailboat. Running.
For someone on the boat, it falls vertically
For someone on the dock, it does not fall vertically.
This is simply the "relativity" of the movement.

Dylan

 

[A.T.]

But Galileo explains that carefully.

You have to decide if you talk about two different scenarios (side kick vs. no side kick) or the same scenario (no side kick) from two different frames (vertical fall vs. parabola).

 

[jbriggs444]

But Galileo explains that carefully.
If something falls from a mast of a sailboat.

Neither @Dale nor myself are arguing against Galilean relativity. The objections we voiced were to an argument that an impulsive sideways kick to a vertically falling object must perform zero work because it is applied over zero distance.

 

[Dylanden]

Hello

Sorry. I just remember about this explanation.
For me a side impulsive kick gives cinetic energy to the object.
And the result is an linear rectilinear motion

Dylan

 

[jbriggs444]

For me a side impulsive kick gives [k]inetic energy to the object.

Or subtracts it. Or leaves it unchanged. Which it is will depend on one's frame of reference.

 

[Dylanden]

Thank you Mr Briggs444

Totaly accord about frame of reference. I understand.

Dylan

 

[Dale]

But Galileo explains that carefully.

I am not sure what point you are trying to make. You cannot transform from a scenario without a kick to a scenario with a kick. They are physically different, not the same thing from different Galilean reference frames.

 

[Dylanden]

Hello Mr Dale

I think you are right.
I will think about the result of a kick.
Carrefully

Dylan

 

[Karagoz]

It is only 90 deg while the object is falling vertically. Once it starts moving off vertical then the horizontal force is no longer at 90 deg.

I didn't get it. Both objects weigh 1Kg, fall free, and fall from 100 meters to the ground.
But the second object gets a kick from the side, so it doesn't fall straight to the ground. We can assume that the force of the kick is 100N applied in 0.02 seconds (an instant kick) on the side (like shown in the picture.

Mechanical energy of an object in free fall is: potential energy + kinetic energy.
When an object is falling free, the potential energy decreases while kinetic energy increase.

So the mechanical energy of the first object is: 1kg * 100m * 9.81 = 981 Joules.

But how do we find the mechanical energy of the second object?

 

[jbriggs444]

I didn't get it. Both objects weigh 1Kg, fall free, and fall from 100 meters to the ground.
But the second object gets a kick from the side, so it doesn't fall straight to the ground. We can assume that the force of the kick is 100N applied in 0.02 seconds (an instant kick) on the side (like shown in the picture.
[...]
But how do we find the mechanical energy of the second object?

100 N for 0.02 seconds. How much impulse is that? If we apply that impulse to a 1 kg object, what horizontal velocity must it have to account for that added momentum? Whatever answer you come up with, let's call it $v_x$.

When doing algebra, it's usually best to leave quantities in symbolic form and substitute known values (100 N, 0.02 seconds, 1 kg, etc) afterward​

At this point there are number of ways to proceed. Let's take an algebraic approach. Say the object has a vertical velocity $v_y$ just prior to the kick. Following the kick its vertical velocity is still $v_y$. Its horizontal is zero just prior to the kick and is $v_x$ afterward.

Kinetic energy just prior to the kick ("initial") is obviously given by: $$E_i=\frac{1}{2}m v_y^2$$
Speed just after the kick is given by the pythagorean formula: $$\sqrt{v_x^2\ +\ v_y^2}$$
Kinetic energy just after the kick ("final") is then given by $$E_f=\frac{1}{2}m\sqrt{v_y^2\ +\ v_x^2}^2 = \frac{1}{2}m v_y^2 + \frac{1}{2}m v_x^2$$
The delta is: $$E_f\ -\ E_i = \frac{1}{2}m v_x^2$$
That's the mechanical energy imparted by the kick.

 

[Dale]

But how do we find the mechanical energy of the second object?

The same way. As you said, KE+PE. The only difference being the different KE due to the work from the kick.