Santilopez10
- 81
- 8
- Homework Statement
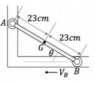
- Point B of a rod of lenght 0.46 m has a constant velocity of 2 m/s to the left. If ##\theta = \frac{\pi}{4}##, find:
a) The angular velocity and acceleration of the rod.
b) The acceleration of the center of mass.
- Relevant Equations
- Rigid body kinematics
we know that the center of instantaneous 0 velocity lies in the interception of 2 perpendicular lines to 2 points, which in this case lies above B. The velocity of any point of the rod can be described relative to the center of instantaneuous 0 velocity ##(Q)## as: $$\vec v_{P/Q}=\vec \omega \times \vec r_{P/Q}$$ For our problem, ##\vec v_{B/Q}=-2 \hat i## ,##\vec r_{B/Q}=-0.46 \sin {\frac{\pi}{4}} \hat j=-0.33 \hat j ## and ## \vec \omega = \omega \hat k ## (We will not assume its sign). Then $$-2 \hat i = 0.33 \omega \hat i \rightarrow \omega = -6 \rightarrow \vec \omega=-6 \hat k$$ This seems physically correct as the rod is rotating clockwise. Before we obtain the angular acceleration we need the velocity of point A, which we can relate to B as ##\vec v_{A/O}=\vec v_{B} + \vec \omega \times \vec r_{A/B}## (Where O is a fixed stationary origin) which ends up being ##\vec v_{A/O}=2 \hat j##.
Let's try to find the acceleration of point A, the equation relating the acceleration of A to B` s is: $$ \vec a_{A/O}= \vec a_{B/O}+ \vec \alpha \times \vec r_{A/B} + \vec \omega \times \vec v_{A/B}$$.
For our case B moves with constant velocity at that instant, ##\vec \alpha = \alpha \hat k##, ##\vec r_{A/B} = -0.33 \hat i +0.33 \hat j##, ##\vec a_{A/O}= a \hat j## and ##\vec v_{A/B} = 2 \hat i + 2 \hat j##. After doing the calculations we arrive at a system of equations: $$
\begin{cases}
-0.33 \alpha +12 =0 \\
-0.33 \alpha -12= a
\end{cases} $$
For which only we are interested in the first. From there we obtain that ##\vec \alpha = 36.36 \hat k##. Here raises my question. Should ##\vec \alpha## be negative for this situation? Or is a positive answer physically correct?
Let's try to find the acceleration of point A, the equation relating the acceleration of A to B` s is: $$ \vec a_{A/O}= \vec a_{B/O}+ \vec \alpha \times \vec r_{A/B} + \vec \omega \times \vec v_{A/B}$$.
For our case B moves with constant velocity at that instant, ##\vec \alpha = \alpha \hat k##, ##\vec r_{A/B} = -0.33 \hat i +0.33 \hat j##, ##\vec a_{A/O}= a \hat j## and ##\vec v_{A/B} = 2 \hat i + 2 \hat j##. After doing the calculations we arrive at a system of equations: $$
\begin{cases}
-0.33 \alpha +12 =0 \\
-0.33 \alpha -12= a
\end{cases} $$
For which only we are interested in the first. From there we obtain that ##\vec \alpha = 36.36 \hat k##. Here raises my question. Should ##\vec \alpha## be negative for this situation? Or is a positive answer physically correct?