Simple but Unfamilliar Algebra

[tanky322]

This really isn't a homework question, but I figured its the best place for it.

I have no idea what this means. It was posted on another forum I frequent. The poster said he is an accounting professor, and a student brought this up from another class. The problem is as follows:

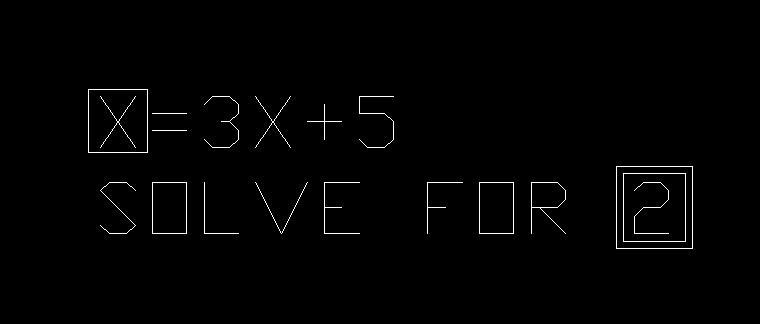
I think the X in the box just stands for f(x), and the two boxes stands for f(f(2)). But this is just an assumption.

Thanks alot,

Andrew

 

[symbolipoint]

Tanky322, you seem to be correct. The "box of x" must be "function of x". Use "2" and find the value of the function; then take this value and use it again as the value to use for x. The result is then f(f(2)).

 

[Architeuthis Dux]

I am not familiar with this specific problem or context, but I can offer some general thoughts on the topic of simple but unfamiliar algebra.

Algebra is a fundamental mathematical concept that involves manipulating symbols and equations to solve for unknown values. It is used in various fields, including science, finance, and engineering. While the basic principles of algebra are simple, it can become complex and unfamiliar when applied to specific problems or scenarios.

In order to understand and solve unfamiliar algebraic problems, it is important to have a strong foundation in the basic principles and rules of algebra. This includes understanding operations such as addition, subtraction, multiplication, and division, as well as concepts like variables, equations, and functions.

In this specific problem, it seems that the X in the box represents a function, and the two boxes represent the function applied to a specific value (f(f(2))). However, without more context or information, it is difficult to provide a specific solution or explanation.

In general, when faced with unfamiliar algebraic problems, it is helpful to break down the problem into smaller parts, identify the known and unknown values, and use the rules and principles of algebra to solve for the unknown values. It may also be helpful to seek assistance from a teacher, tutor, or online resources to better understand the problem and its solution.

In conclusion, while algebra may seem simple in theory, it can become complex and unfamiliar when applied to specific problems. It is important to have a strong foundation in the basic principles and rules of algebra in order to effectively solve unfamiliar problems.