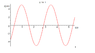
SUMMARY
The discussion focuses on determining the initial phase angle of a graph representing simple harmonic motion (SHM). Participants emphasize the importance of understanding the relationship between the phase angle and the graph's characteristics, particularly how it translates the graph along the time axis. A reference to equation 510 from a physics resource is highlighted as a useful tool for finding the phase angle. The conversation also notes that a phase angle of zero corresponds to a cosine graph, indicating maximum amplitude at the start.
PREREQUISITES
- Understanding of Simple Harmonic Motion (SHM)
- Familiarity with phase angles in oscillatory motion
- Knowledge of graph interpretation in physics
- Basic understanding of trigonometric functions, particularly cosine
NEXT STEPS
- Study the derivation and application of equation 510 related to phase angles in SHM
- Learn how to analyze displacement vs. time graphs for SHM
- Explore the relationship between phase angles and maximum amplitude in oscillations
- Review resources on the theory of Simple Harmonic Motion for deeper comprehension
USEFUL FOR
Students studying physics, particularly those focusing on oscillatory motion, as well as educators seeking to clarify concepts related to phase angles in simple harmonic motion.