Simple wave problem - phase constant

[i_hate_math]

Homework Statement

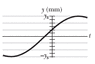
The figure shows the displacement y versus time t of the point on a string at x = 0, as a wave passes through that point. The scale of the x axis is set by ys = 84.0 mm.The wave has form y(x, t) = ym sin (kx - ωt+φ). What is φ? (Caution: A calculator does not always give the proper inverse trig function, so check your answer by substituting it and an assumed value of ω into y(x, t) and then plotting the function.)

Homework Equations

y(x, t) = ym sin (kx - ωt+φ)

The Attempt at a Solution

This is supposed to be really easy but the solution I got was wrong. My approach was straight forward:
read off the initial y value --- y(0,0)=0.028
and sub in the equation: 0.028=0.084sin(0-0+φ)
φ=arcsin(0.028/0.084)=0.339836...=0.340 rad
The question mentioned that the calculator might give the wrong value but I do not see how I could make amend to it.
Please enlighten me!

 

[blue_leaf77]

At $x=0$, you have $y = -A\sin(\omega t -\phi)$, this is the curve $y = -A\sin(\omega t)$ translated by $\phi$. When you compare $y = -A\sin(\omega t)$ with the picture you uploaded, you should see that $\phi$ should be in the second quadrant.

 

[i_hate_math]

At $x=0$, you have $y = -A\sin(\omega t -\phi)$, this is the curve $y = -A\sin(\omega t)$ translated by $\phi$. When you compare $y = -A\sin(\omega t)$ with the picture you uploaded, you should see that $\phi$ should be in the second quadrant.

I see where I went wrong, thank you very much for the help!

 

[i_hate_math]

At $x=0$, you have $y = -A\sin(\omega t -\phi)$, this is the curve $y = -A\sin(\omega t)$ translated by $\phi$. When you compare $y = -A\sin(\omega t)$ with the picture you uploaded, you should see that $\phi$ should be in the second quadrant.

Though, are you sure its in the second quadrant? I think it should be π+0.340 and that's third quadrant

 

[blue_leaf77]

I think it should be π+0.340 and that's third quadrant

That cannot be the case because sine of an angle in 3rd quadrant is negative, on the other hand the displacement is positive in your picture.

 

[i_hate_math]

That cannot be the case because sine of an angle in 3rd quadrant is negative, on the other hand the displacement is positive in your picture.

So it would be π-0.34? This gives a value that's in the 2nd quad

 

[blue_leaf77]

Yes.