Discussion Overview
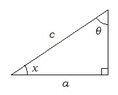
The discussion revolves around simplifying the expression $$\sin^{-1}(\cos(x))$$ using a right triangle. Participants explore the implications of the expression and how it relates to trigonometric identities and relationships between angles.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
- Homework-related
Main Points Raised
- Some participants clarify that the expression $$\theta=\sin^{-1}(\cos(x))$$ is the focus, while others suggest it might be a typo and that $$y=\sin(\cos^{-1}(x))$$ was intended instead.
- One participant notes that taking the sine of both sides leads to $$\sin(\theta) = \cos(x)$$, prompting questions about the relationship between $$\theta$$ and $$x$$.
- Another participant mentions the identity $$\sin^2\theta+\cos^2\theta=1$$ as relevant for simplifying $$\sin(\cos^{-1}(x))$$, but not for $$\sin^{-1}(\cos(x))$$.
- Some participants discuss the implications of drawing a right triangle and how it relates to the angles involved, suggesting that if $$\sin(\theta) = \cos(x)$$, then $$\theta$$ and $$x$$ are complementary angles.
- There is a suggestion that $$x + \theta = 90^{\circ}$$ or $$x + \theta = \frac{\pi}{2}$$, leading to the conclusion that $$x = \frac{\pi}{2} - \theta$$.
- Participants express uncertainty about the necessity of drawing a triangle for the problem and whether the original question was correctly stated.
Areas of Agreement / Disagreement
Participants generally agree that there may be a typo in the problem statement, but they also explore the implications of the expression as given. The discussion remains unresolved regarding the intended expression and the necessity of using a triangle for simplification.
Contextual Notes
Some participants note that the simplification of $$\sin^{-1}(\cos(x))$$ may require additional considerations for all values of $$x$$, particularly regarding the range of the inverse sine function.