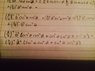Simplify with Trigonometric Identities

[KleZMeR]

Homework Statement

I'm trying to simplify some trigonometric expressions, I'm attaching my work here. This comes from a famous physics problem i.e. the rod with two masses spinning on a circle. I've tried many times but I just can't get it. Any help on which identities to use would really help me.

Homework Equations

I'm attaching the simplified version, the 'answer'

The Attempt at a Solution

I'm attaching my work.

 

[NascentOxygen]

Apply a couple of times sin² x + cos² x = 1
and your last line simplifies to the given answer

 

[KleZMeR]

Apply a couple of times sin² x + cos² x = 1
and your last line simplifies to the given answer

Yes, I looked at that identity, but there are 2 different angles in this problem, and also one of my last two terms is dø²*sin²Θ

Any direction on how to first apply the identity would also help?

 

[NascentOxygen]

Take cos² θ outside some brackets because it's a common factor.

And you'll see again, there's another common factor in two other terms to treat similarly.