Simultaneity in 2 spatial dimensions

[JVNY]

Homework Statement

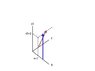
Two objects, Red and Blue, are in inertial motion with respect to each other and are graphed on the attached Minkowski diagram (representing a third inertial frame). Red and Blue are in relative motion along the x axis, and offset slightly on the z axis such that they will not collide when passing each other. At ct=2, Red and Blue have the same x coordinate, x=1. The question is: will Red and Blue agree on the simultaneity of any two or more events that occur at any points on the z axis that also have ct and x coordinates of ct=2, x=1?

Homework Equations

Not applicable.

The Attempt at a Solution

I believe that yes, Red and Blue will agree on the simultaneity of events that occur at ct=2, x=1, and z=any number. I think that the relativity of simultaneity only applies to events separated in space along the axis of motion; similarly, length contraction and time dilation also occur only along the axis of motion. If I am correct about this then I would have a follow up question, because if they agree on simultaneity then it raises another question about one of the relativity paradoxes.

Thanks in advance for any help.

 

[TSny]

The question is: will Red and Blue agree on the simultaneity of any two or more events that occur at any points on the z axis that also have ct and x coordinates of ct=2, x=1?

If x = 1 for the event, then the event can't be on the z axis.

I believe that yes, Red and Blue will agree on the simultaneity of events that occur at ct=2, x=1, and z=any number.

That sounds correct to me. The Lorentz transformation equations can be used to prove it.

 

[JVNY]

Thanks. If I might, here is a follow up question.

There are various explanations of the Ehrenfest Paradox, such as that the geometry of a rotating disk or cylinder is not Euclidean. In what may be a different explanation, "Grøn states that the resolution of the paradox stems from the impossibility of synchronizing clocks in a rotating reference frame." See http://en.wikipedia.org/wiki/Ehrenfest_paradox.

It seems that the opposite ends of a diameter of a circle undergoing uniform circular motion are like Red and Blue above. At any instant, their velocities are opposite each other and are always orthogonal to the diameter (see attachment from wikipedia). So it would seem that the opposite ends of the diameter would agree on the simultaneity of events anywhere on the diameter. As a result, one could synchronize clocks on the ends of any given diameter of a rotating circle.

So is it possible to synchronize clocks on the ends of a diameter of a rotating circle? It seems to be possible, but it would be contrary to Gron's view (at least for the limited case of the ends of a diameter).

Thanks in advance.

 

[TSny]

Right, you cannot arrange for all the clocks on the rim to be synchronized with each other according to the rotating frame. But I think you can arrange for all diametrically opposite clocks to be synchronized with each other in the following sense.

Let the “lab” frame be the non-rotating inertial frame in which the center of the disk is at rest.
Suppose that at t = 0 according to the lab frame, each clock on the rim is set to t = 0. So, at t = 0 in the lab frame, all clocks on the rim also read t = 0. Then all of the clocks on the rim are synchronized with each other according to the lab frame. In the lab frame, the rim clocks will run slow but they all will remain synchronized with each other.

Let A and B be two diametrically opposite clocks on the rim. If an observer is riding on the rim at the location of A, will she consider B to be synchronized with A? It depends on the definition of simultaneity that one uses for such an accelerating observer. One definition would be to use a co-moving inertial frame.

Thus at the instant the clock at A reads 1.0 s we image an inertial frame that is co-moving with A at that instant. Then, according to this co-moving inertial frame, the diametrically opposite clock B will read 1.0 s simultaneously with clock A reading 1.0 s. See if you can justify this statement using the result of your first post. So, if the observer riding on the rim at A agrees to use the co-moving inertial frame to decide on what clock B reads at the “same time” clock A reads a certain value, then the rim rider at A will say that B is synchronized with A.

Clearly, the same argument holds for any two diametrically opposite clocks. So, in this sense, you could say the diametrically opposite clocks in the rotating frame are synchronized. However, this does not imply that clocks that are not diametrically opposite are synchronized in the rotating frame.

 

[JVNY]

Yes, I agree with you. The circle should present length contracted to every rim rider parallel to the rider's direction of travel (thus like an ellipse, perhaps); and the clocks on the other points would then not be synchronous with the two ends of the diameter. So it does seem that Gron is partially right, but incorrect as to the ends of any diameter.

Also, it seems as if there is an analogy to gravity and to a row of points accelerating Born rigidly. If there were a rotating disk (rather than a circle), every point on the given diameter could be synchronized at inception to t=0, like the end points. Then, going forward, all clocks on the diameter would agree on simultaneity of events, although (a) the closer a clock is to the center the faster it will run, and (b) every pair of clocks on the diameter equidistant from the center would run at the same rate. It seems that one could treat the case of the diameter as similar to gravity (with the gravitational mass being equivalent to the center of the disk), and that one can treat the points along a radius like a row of points accelerating Born rigidly (each point agrees on the simultaneity of events, but clocks run faster the closer they are to the center of the disk or to the front of the row of Born rigidly accelerating points).

Thanks again.

 

[TSny]

What you say sounds good to me.

For the interpretation in terms of a gravitational potential, I guess the mass at the center of the disk would need to be "negative" to produce radially outward force on objects in the rotating frame and to cause clocks closer to the center to run faster. But I get your point.

 

[JVNY]

Yes, sorry about getting that backwards!