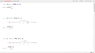
##\frac{ m v^2} R ≤ kmg ##
##v≤ \sqrt {k g R} ##
So, the maximum allowed speed is ##v_{mx} = \sqrt { k g R_{mn} }##
where R
mn is the minimum radius of curvature
If the curve is given in
Cartesian coordinates as
y(
x), then the radius of curvature is (assuming the curve is differentiable up to order 2):
## R = | \frac { \left ( 1 + y' ^2\right )^ \frac 3 2 } { y" }| ##
R
mn, turns out to be radius of curvature at that point where Sine function has maximum value. So, the curve is a straight line. And radius of curvature of straight line is infinity, right? So, where am I wrong?
I copied these latex codes from mathematica. Now how to bring it in the standard form?
\documentclass{article}
\usepackage{amsmath, amssymb, graphics, setspace}
\newcommand{\mathsym}[1]{{}}
\newcommand{\unicode}[1]{{}}
\newcounter{mathematicapage}
\begin{document}
\begin{doublespace}
\noindent\(\pmb{\text{}}\)
\end{doublespace}
\begin{doublespace}
\noindent\(\pmb{\text{}}\)
\end{doublespace}
\begin{doublespace}
\noindent\(\pmb{\text{}}\\
\pmb{}\\
\pmb{y= a \text{Sin}[x/\alpha ]}\)
\end{doublespace}
\begin{doublespace}
\noindent\(a \text{Sin}\left[\frac{x}{\alpha }\right]\)
\end{doublespace}
\begin{doublespace}
\noindent\(\pmb{y'= D[y,x]}\)
\end{doublespace}
\begin{doublespace}
\noindent\(\frac{a \text{Cos}\left[\frac{x}{\alpha }\right]}{\alpha }\)
\end{doublespace}
\begin{doublespace}
\noindent\(\pmb{y\text{''} = D[y',x ]}\)
\end{doublespace}
\begin{doublespace}
\noindent\(-\frac{a \text{Sin}\left[\frac{x}{\alpha }\right]}{\alpha ^2}\)
\end{doublespace}
\begin{doublespace}
\noindent\(\pmb{R = \{(1+ y' {}^{\wedge}2){}^{\wedge}(3/2 ) \}/y\text{''}}\)
\end{doublespace}
\begin{doublespace}
\noindent\(\left\{-\frac{\alpha ^2 \left(1+\frac{a^2 \text{Cos}\left[\frac{x}{\alpha }\right]^2}{\alpha ^2}\right)^{3/2} \text{Csc}\left[\frac{x}{\alpha }\right]}{a}\right\}\)
\end{doublespace}
\begin{doublespace}
\noindent\(\pmb{\text{DSolve}[R'[x] =0, x]}\)
\end{doublespace}