Magnetic field due to a straight wire and circular arc

[Victim]

Homework Statement

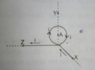
Find the magnitude of the magnetic induction B of a magnetic field generated by a system of thin conductors along which a current i is flowing at a point A(O,R,O), that is the center of a circular conductor of radius R. The ring is in the yz plane.

Homework Equations

[/B]
magnetic field due to a straight wire=μ₀i/4πr [sinθ₁ + sinθ₂]
magnetic field due to circular arc=μ₀i/2r

The Attempt at a Solution

 

[BvU]

On your illegible attempt -- please post it as text or $\LaTeX$ -- I see four terms.
Why four ? Where does each come from ?

 

[Victim]

On your illegible attempt -- please post it as text or $\LaTeX$ -- I see four terms.
Why four ? Where does each come from ?

please don't reply when you don't know the answer

 

[kuruman]

magnetic field due to a straight wire=μ₀i/4πr [sinθ₁ + sinθ₂]

How do you figure? What are angles θ₁ and θ₂?

please don't reply when you don't know the answer

This was unnecessary, @BvU was trying to help you get to the answer as am I. To help you, we need first to understand where you're coming from and what your difficulties are. If, however, you want to know just the answer to this problem, you will not get it here. It is against our rules to give out answers. Please read them
https://www.physicsforums.com/threads/guidelines-for-students-and-helpers.686781/

 

[Victim]

I read.I had not break any rules.
I had post a clear image.
I had given my attempt clearly.

 

[Charles Link]

I passed on responding because the second image is sideways. Meanwhile, the calculation of the solution will involve computing both a magnitude plus a direction of the magnetic field from the 3 sources that contribute to it. It would help to at least get the image that you post right side up.

 

[kuruman]

I read.I had not break any rules.
I had post a clear image.
I had given my attempt clearly.

I never said or implied that you broke any rules. I said that our rules do not allow us to give away answers. We cannot help you if you will not let us do so by answering our questions.

I passed on responding because the second image is sideways. Meanwhile, the calculation of the solution will involve computing both a magnitude plus a direction of the magnetic field from the 3 sources that contribute to it. It would help to at least get the image that you post right side up.

Posting the same figure rotated by 90^o will not be much help. I studied the figure on my rotated laptop. It shows four contributions, two in the $\hat i~$ direction and two in the $\hat k~$ direction. That cannot be if the wire assembly is all in the same plane. OP needs to explain how these are derived as @BvU observed.

On edit: I understand the geometry now, but I still don't understand why four contributions.

 

[Victim]

I passed on responding because the second image is sideways. Meanwhile, the calculation of the solution will involve computing both a magnitude plus a direction of the magnetic field from the 3 sources that contribute to it. It would help to at least get the image that you post right side up.

The image is sideways but each and every letter can be read easily.Tell me the word or number which you can't read.

 

[Victim]

The image is sideways but each and every letter can be read easily.Tell me the word or number which you can't read.

are you not able to see in the image that one wire is on x-axis and one wire is in z axis.

 

[Charles Link]

We see plenty and plenty of homework problems on Physics Forums, and many of them, like this one, are not very difficult. One thing we always like to see is a willingness on the part of the OP (OP=original poster=person submitting the post) to put a little bit of effort into working the problem, and making it a little bit easy on the homework helpers. In this case, that effort seems to be lacking.

 

[BvU]

please don't reply when you don't know the answer

I know the answer, as do you. When I almost break my neck sideways I can see it's written at the bottom of your page.

You still have not explained how you get 4 terms out of three contributions.

You may not have broken any rules yet, but you should read the guidelines (in particular item 5) about helping the helpers. As opposed to ticking them off because you feel you aren't being served properly or not getting your money's worth

 

[Victim]

I know the answer, as do you. When I almost break my neck sideways I can see it's written at the bottom of your page.

You still have not explained how you get 4 terms out of three contributions.

You may not have broken any rules yet, but you should read the guidelines (in particular item 5) about helping the helpers. As opposed to ticking them off because you feel you aren't being served properly or not getting your money's worth

dont you remember that a(x+y) =ax + ay
see attached image again

 

[BvU]

I remember. But there is no relation to your exercise. I don't see a $\vec B$ at a $\pi/4$ angle

 

[Victim]

I remember. But there is no relation to your exercise. I don't see a $\vec B$ at a $\pi/4$ angle

you leave it.you cannot do.why do you need B at π/4 angle

 

[Delta2]

Here is the image rotated properly. Still I find it very hard for my eyes and my brain to understand it.
Maybe the other helpers find it easier to help now.

 

[BvU]

you leave it.you cannot do

What makes you think that ?
Anyway, this is your thread and I do hope you really want help with this exercise. Why don't you do the wise thing and read the advice (again, if you already did) from three heavyweights and try to follow it, instead of working yourself up into a blocking frustration.

You write $$\vec B = {\mu_0\,i \over 4\pi\, r}\; ( {\bf -\hat k} )+ {\mu_0\,i \over 4\pi\, r} \; ( {\bf -\hat \imath} ) + {\mu_0\,i \over 2\, r} \; {-( \bf -\hat\imath + \hat k) \over ??} $$ and all we humbly ask of you is to explain where these terms come fromDelta, thanks for rotating the picture. My desktop screen is too heavy to turn over $\pi/2$ !

Now I see the curly $h$ is in fact $\sqrt 2 \quad$

 

[Charles Link]

The ring is in the y-z plane according to the OP=original post. That means the direction of the unit vector in the 3rd term is is the wrong direction. ($\hat{u}=\frac{-\hat{i}+\hat{k} }{\sqrt{2} }$ is incorrect. (This is the 45 degree angle=$\frac{\pi}{4}$ (radians) that is being referred to in the discussion above). $\\$ It looks like the OP is presently off the air with a line through his name.

 

[BvU]

Giving it away, eh ? tut tut

 

[Delta2]

when there is a line through a user name it means that the user got banned, or he deleted his account?

 

[BvU]

I wonder how that came to happen ...

 

[berkeman]

when there is a line through a user name it means that the user got banned, or he deleted his account?

He is temp banned for multiple infractions over a period of time. Thanks for trying to help, all. Hopefully when he comes back in 10 days, he will abide by the PF rules.

Thread is closed.