SUMMARY
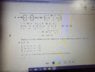
The discussion focuses on determining the singularity of a 3x3 matrix through row operations on its determinant. Key operations include replacing a row with the sum of itself and another row, switching two rows, and multiplying a row by a scalar. The participants clarify that while replacing R1 with R1 + R3 alters the value of R1, it simplifies the determinant calculation by introducing a zero entry. The conclusion emphasizes that a system yielding a contradiction, such as 0 = 3, indicates inconsistency and no solutions.
PREREQUISITES
- Understanding of matrix operations, specifically row operations.
- Familiarity with determinants and their properties.
- Basic knowledge of linear algebra concepts, including systems of equations.
- Ability to interpret mathematical contradictions in equations.
NEXT STEPS
- Study the properties of determinants in linear algebra.
- Learn about row echelon form and its applications in solving systems of equations.
- Explore the implications of inconsistent systems in linear algebra.
- Investigate geometric interpretations of determinants, such as area and volume calculations.
USEFUL FOR
Students and educators in mathematics, particularly those studying linear algebra, as well as anyone interested in understanding matrix singularity and determinant calculations.