Engineering Sinusoidal steady state analysis using Laplace transform

[Wrichik Basu]

Homework Statement

Find $i_x(t)$ in the given circuit at the steady state.

Relevant Equations

Laplace transforms for circuit elements. $$\begin{align}
t\mathrm{-domain} &\rightarrow s\mathrm{-domain}\\
R &\rightarrow R \\
L &\rightarrow sL \\[0.9em]
C &\rightarrow \dfrac{1}{sC}\\[0.9em]
\cos \omega t &\rightarrow \dfrac{s}{s^2 + \omega^2} \\[0.9em]
\sin \omega t &\rightarrow \dfrac{\omega}{s^2 + \omega^2}
\end{align}$$

$\require{physics}$The given circuit is this:

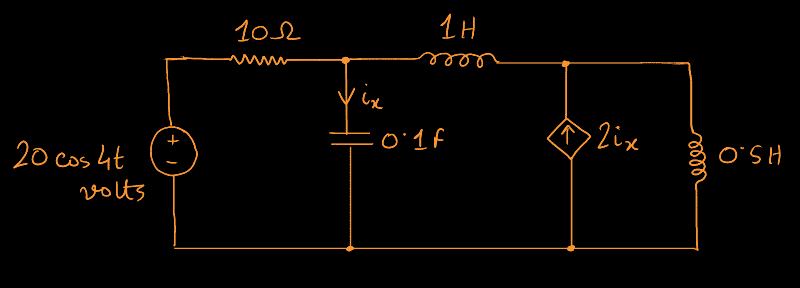
The question is taken from this video. The Professor has solved it using Phasor analysis, the final solution being $$\begin{equation}
i_x(t) = 7.59 \sin \qty( 4t + 108.4^\circ )~\mathrm{amps}.
\end{equation}$$My aim, however, is to use Laplace transform to reproduce this solution.

Step 1 is to transform all the circuit elements from the time domain to the frequency domain. The transformed circuit looks like:

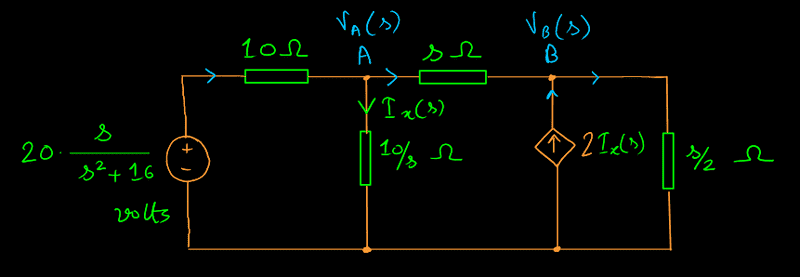
At node A,$$\begin{align}
&\phantom{implies} \dfrac{\dfrac{20 s}{s^2 + 16} - V_A(s)}{10} - I_x(s) - \dfrac{V_A - V_B}{s} = 0 \nonumber \\[0.8em]
&\implies \dfrac{2s}{s^2 + 16} - \dfrac{V_A}{10} - \dfrac{V_A}{10/s} - \dfrac{V_A - V_B}{s} = 0.\label{eqn1}
\end{align}$$
At node B,$$\begin{align}
\dfrac{V_A - V_B}{s} + 2\dfrac{V_A}{10/s} - \dfrac{V_B}{s/2} = 0.\label{eqn2}
\end{align}$$
Solving equations$~\eqref{eqn1}$ and $\eqref{eqn2}$ yield $$\begin{align}
V_A(s) &= \dfrac{60 s^2}{\qty( s^2 + 16 ) \qty( s^2 + 3s + 2)} \\[0.8em]
\implies I_x(s) &= \dfrac{6s^3}{\qty( s^2 + 16 ) \qty( s^2 + 3s + 2)}.
\end{align}$$
Time to take the inverse Laplace transform. $$\begin{align}
I_x(s) &= \dfrac{6s^3}{\qty( s^2 + 16 ) \qty( s^2 + 3s + 20)} \nonumber \\[1em]
&= \dfrac{\dfrac{42}{5}s + 36}{s^2 + 3s + 20} - \dfrac{\dfrac{12}{5}s + \dfrac{144}{5}}{s^2 + 16} \nonumber \\[1em]
&= \dfrac{\dfrac{42}{5}\qty( s + 1.5 )}{\qty( s + 1.5 )^2 + \dfrac{71}{4}}
+ \dfrac{234}{5\sqrt{71}} \dfrac{\sqrt{71}/2}{\qty( s + 1.5 )^2 + \dfrac{71}{4}} - \dfrac{12}{5} \qty[ \dfrac{s}{s^2 + 16} + 3 \dfrac{4}{s^2 + 16} ] \nonumber\\[1em]
\implies i_x (t) &= \dfrac{42}{5} \exp^{-1.5t} \qty[ \cos \qty( \dfrac{\sqrt{71}}{2}t ) + \dfrac{39 \sqrt{71}}{497} \sin \qty( \dfrac{\sqrt{71}}{2}t ) ] - \dfrac{12}{5} \qty[ \cos (4t) + 3 \sin (4t) ].
\end{align}$$
At steady state, i.e. when $t \rightarrow \infty,$ the exponential part vanishes, so I am left with only $$\begin{equation}
i_x (t) = - \dfrac{12}{5} \qty[ \cos (4t) + 3 \sin (4t) ]~\mathrm{amps}. \label{eqn:ixt_final}
\end{equation}$$

I am not sure how to proceed from here to arrive at the same equation that was derived in the video.

If I plot the two values, I get

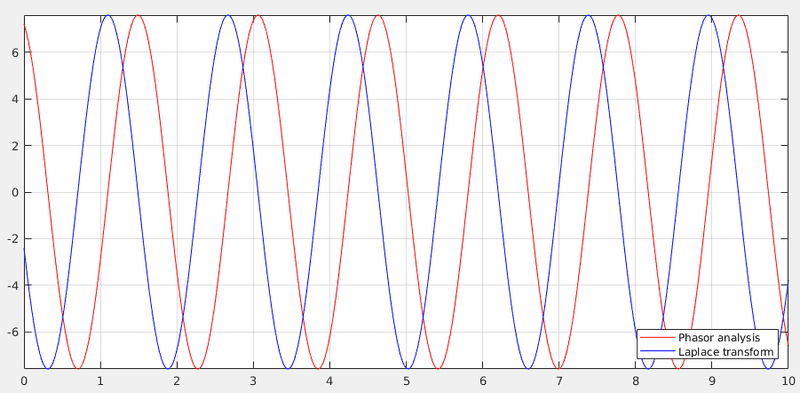
which is just a phase difference. I am not sure where I went wrong. Any leads will be helpful.

 

[gneill]

Since your source voltage is of the form $20 \cos(4 t)$, I believe that your steady state answer should also be in that form:
$$ i_x(t) = 7.59 \cos \qty( 4t + 108.4^\circ )~\mathrm{amps}$$
So I think that your professor mistook the sin for cos. This, will I believe solve your phase difference issues between the phasor approach and the Laplace approach.

 

[Wrichik Basu]

Since your source voltage is of the form $20 \cos(4 t)$, I believe that your steady state answer should also be in that form:
$$ i_x(t) = 7.59 \cos \qty( 4t + 108.4^\circ )~\mathrm{amps}$$
So I think that your professor mistook the sin for cos. This, will I believe solve your phase difference issues between the phasor approach and the Laplace approach.

That sure does solve the issue. Thank you!

 

[gneill]

You're very welcome!