Sliding Ramp and Freefall problem

Click For Summary

Homework Help Overview

The discussion revolves around a physics problem involving a sliding ramp and freefall, specifically focusing on determining the height of the ramp (h) based on the motion of an object as it transitions from the ramp to freefall. The problem involves concepts from kinematics and dynamics, particularly the components of motion along an incline.

Discussion Character

  • Exploratory, Conceptual clarification, Mathematical reasoning, Problem interpretation, Assumption checking

Approaches and Questions Raised

  • Participants discuss the components of velocity at the end of the ramp and how to relate them to the height h. There are attempts to use kinematic equations and energy conservation principles, but confusion arises regarding the variables involved and their relationships.

Discussion Status

Multiple interpretations of the problem are being explored, with some participants suggesting algebraic expressions for velocity in terms of h. Guidance has been offered regarding the use of free body diagrams and the importance of maintaining clarity with variables. However, there remains a lack of consensus on how to proceed with the calculations.

Contextual Notes

Participants note constraints such as the absence of certain numerical values and the requirement to solve the problem using only the knowledge of kinematics, as conservation of energy has not yet been covered in their studies. There is also confusion regarding the definitions of h and Δh in the context of the ramp's geometry.

Shaku
Messages
46
Reaction score
0
I typed this up on MP's Whiteboard, but the tutors were taking way too long to respond:
(question is also attached)

Edit:
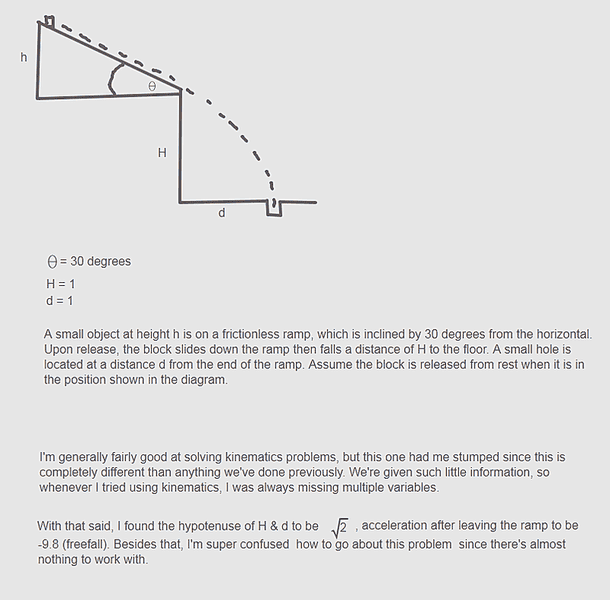
Units are in meters.
Questions asks to Find h (small h defining the height of the ramp).
The exact moment the object leaves the ramp, it would have components Y=gsin(30) and X=gcos(30).

1zvbps5.png
 

Attachments

  • help.png
    help.png
    34.2 KB · Views: 768
Last edited:
Physics news on Phys.org
The motion starts with the incline, so it is useful to start the analysis there as well.
What do you know about the object at the end of the incline?
You can use this for the free fall afterwards.

Do you have any units for your values? Like... meters?
 
Yeah, I already tried that -- but I'd still be missing variables to do anything useful with the x and y components. It would be gsin(30) but I'm not sure where to go from there.

Units are in meters, and the problem has to solve for h (the small "h" defining the ramp's height).
 
Last edited:
In terms of h, what will the horizontal and vertical components of velocity be at the end of the ramp? (You can either determine the acceleration down the ramp or use conservation of energy.)
 
gsin(30) and gcos(30). But what am I supposed to do with that information? I'm still confused as we're supposed to reach an actual numerical answer for h.
 
Shaku said:
gsin(30) and gcos(30).
Those are the accelerations. What about the velocities at the end of the ramp?
I'm still confused as we're supposed to reach an actual numerical answer for h.
You are.
 
That's the problem I'm running into which I'm confused about -- I don't have enough information there to use kinematics to figure that out.

I don't have distance of the length adjacent to the angle, and I don't have time.

Δs = vi*t + (1/2)at^2

Which leaves me with three unknowns (time, velocity, and Δs).
 
Shaku said:
I don't have distance of the length adjacent to the angle
Not numerically, no, but you have the unknown h. Use that. You only need an algebraic expression for velocity as a function of h. It doesn't matter that you don't yet know the value of h.
 
So, I would have:

Δh = 0(t) + (1/2)(a)(t)
= (1/2)(gSin(30)(t)^2
= (49/20)t^2

[STRIKE]Differentiating, I would get:

Δh = 2(49/20)t
= 4.9t[/STRIKE]

Where do I go from here? I don't know the time since it is an unknown variable. How would I go about finding the height once I have this equation?
 
Last edited:
  • #10
Can you find the velocity (horizontally and vertically) at the end of the ramp as function of h? The determined value for the time can help.
 
  • #11
Could you clarify what you mean? I found the function of h to be Δh = 4.9t...

These question-as-an-answer type responses are just confusing me more and more. I appreciate the help, but I'd more-so appreciate it if someone could try not being so cryptic in their responses.
 
  • #12
No, that formula does not make sense. You cannot just derive one side, and ignore the other side.

Δh = (49/20)t^2
This is a relation between the length of the ramp and the time the object needs to go down. As you know the acceleration, what is the final velocity after that time?
How are the length of the ramp ("Δh") and h related? They are not the same...
 
  • #13
Ohhhh, that makes much more sense.

Vfy = Vi + a(t)
Vfy = 0 + gSin(30)*(t)
Vfy = 4.9t

So I know:
ay = 4.9
Viy = 0
Vfy = 4.9t
Δh = (49/20)t^2

Plugging those values back in, I get:
Vf = Vi(t) + a(t)
4.9t = 0 + 4.9t

or

Δh = Vi(t) + (1/2)(a)(t)^2
(49/20)t^2 = 0 + (49/20)t^2

Which just cancels out if I try to do anything with that information... I'd guess that I would have to somehow figure out the time, and then use the time to figure out what Δh's length is. Using Δh's length and the angle, I'd be able to find h.

But I'm still very confused since I don't know how to proceed from here.
 
  • #14
Vf=4.9t

You can solve Δh = (49/20)t^2 for t and plug it into the first equation. This gives Vf as function of Δh.
Using Δh's length and the angle, I'd be able to find h.
Right. Therefore, the first step is a relation Vf = (some expression with just h).
You can ignore the time in your equations if you know how to use energy conservation.

Once you have that: Vf is in the direction of the slope. Can you split it in a horizontal and a vertical component? Those are the initial conditions for the free fall afterwards.
 
  • #15
Solving for t, I get:
Δh = (49/20)t^2
[Δh/(49/20)] = t^2
sqrt[Δh/(49/20)] = t

Plugging into the first equation, I get:
Vfy = (4.9)(sqrt[Δh/(49/20)])

We haven't learned conservation of energy yet; just general kinematics.

So now that I have Vfy as a function of Δh, how do I use that to solve for h?
If I plug in this Vfy as Viy of the freefall portion, I would still be missing too many variables to solve for anything on the y axis.
I'd be missing the same information on the x-axis too. We haven't learned conservation of energy yet -- when we were given this problem, it was given to us as-is.
We have to it solve with our current knowledge of kinematics.
 
  • #16
how do I use that to solve for h?
You know the angles in the triangle...

If I plug in this Vfy as Viy of the freefall portion, I would still be missing too many variables to solve for anything on the y axis.
You can find enough equations. Just keep on working with the variables*, you can solve for h at the end of the calculations.

*by the way: I think it would be easier to keep g as parameter as well, instead of using things like 49/20.
 
  • #17
I'm confused again... I tried:

Plugging t into distance equation:
Δs = Vi(t)+(1/2)(a)(t)^2
Δh = 0 + (1/2)(gSin(30)(sqrt(Δh/2.45))^2
=(1/2)(gSin(30)(sqrt(Δh/2.45))
Δh = Δh ...?

Could you clarify what variables I'm trying to solve for, and how I'm supposed to solve for them? I tried a few different ideas, but I always ended up with strange numbers/variables that didn't work.

Here's what I have so far:
y2q1e.jpg
 

Attachments

  • help2.jpg
    help2.jpg
    18.9 KB · Views: 618
Last edited:
  • #18
Let's back up here for a moment. Just realized I didn't check something you wrote earlier: you gave the components of the acceleration as gsin(30) and gcos(30). They're wrong.
Draw the free body diagram of the block. What are the forces on it?
Shaku said:
Vfy = (4.9)(sqrt[Δh/(49/20)])
I don't know why you changed "h" to "Δh". They seem to be the same thing, and you created some confusion by doing that. Also, as mfb says, it's much clearer to stick with symbols, like g, and leave the numbers until the end. It's easier to spot mistakes too. Ideally you should do that with the angles too, i.e. leave sin(30) as that instead of substituting 1/2, but I'll allow an exception there.
We haven't learned conservation of energy yet; just general kinematics.
In many situations, including this one, C of E is the same as the kinematic equation vf2 = vi2+2as.
 
  • #19
haruspex said:
Let's back up here for a moment. Just realized I didn't check something you wrote earlier: you gave the components of the acceleration as gsin(30) and gcos(30). They're wrong.
Draw the free body diagram of the block. What are the forces on it?

It is a frictionless ramp and the object starts at rest. The only force would be gravity, and the momentum it gains in the x-direction which is gCos(30).

haruspex said:
I don't know why you changed "h" to "Δh". They seem to be the same thing, and you created some confusion by doing that. Also, as mfb says, it's much clearer to stick with symbols, like g, and leave the numbers until the end. It's easier to spot mistakes too. Ideally you should do that with the angles too, i.e. leave sin(30) as that instead of substituting 1/2, but I'll allow an exception there.

Isn't Δh the hypotenuse of the ramp (aka, the ramp's length itself), and h is the height from which the object was released?

In many situations, including this one, C of E is the same as the kinematic equation vf2 = vi2+2as.

Wouldn't this just be the same as plugging the original two kinematic equations together (which is what I did here)?

It just end up being what I already had:
Vf = (4.9)(sqrt[Δh/(49/20)])
 
  • #20
Shaku said:
I'm confused again...
You try to solve everything at once, or insert equations into itself. That won't help.
Just consider what you have, and what you do not have yet, and how to connect them.

Look at your triangle, for example: How are h, the angle and Δh connected?
Ignore all other parts of the problem here!
 
  • #21
Shaku said:
It is a frictionless ramp and the object starts at rest. The only force would be gravity, and the momentum it gains in the x-direction which is gCos(30).
No it isn't. Which way are you resolving forces to arrive at that? Vertically and horizontally or normally and tangentially to the ramp? You can do either, but you seem to be doing one then misinterpreting the answer as though you had done the other.
Isn't Δh the hypotenuse of the ramp ?
It is if you define it that way. I didn't see any such definition. If I missed it I apologise. But I think that approach will get messy - just use vertical and horizontal distances, not hypotenuse distances.
 
  • #22
mfb said:
Look at your triangle, for example: How are h, the angle and Δh connected?
Ignore all other parts of the problem here!

If we're talking just about this part of the problem, h would be:
h = Δh*Sin(30)

But Δh is in terms of t, which I don't have, so it would just become:
h = 4.25t2*Sin(30)

It makes sense that everything is connected, but I'm having a hard time putting the pieces together since there are still two unknowns which make it difficult to solve for h.

Could you clarify what steps I have left to do?
 
  • #23
haruspex said:
No it isn't. Which way are you resolving forces to arrive at that? Vertically and horizontally or normally and tangentially to the ramp? You can do either, but you seem to be doing one then misinterpreting the answer as though you had done the other.

Maybe you should read the problem... It states that it is a frictionless ramp (and yes, I know, there is no such thing as a "frictionless ramp," but for the sake of the problem, there is no friction).

It is if you define it that way. I didn't see any such definition. If I missed it I apologise. But I think that approach will get messy - just use vertical and horizontal distances, not hypotenuse distances.

If you read through the replies of the other forum members, we defined it as the hypotenuse. It does require an extra mathematical expression at the end though to find h... But I wasn't sure how to define the horizontal distance since there wasn't enough information to relate to that easily. I just found the hypotenuse to be easier to work with, with the given information (or lack thereof!).
 
  • #24
Shaku said:
It states that it is a frictionless ramp
I'm aware of that, and your expressions for horizontal and vertical accelerations are still wrong. Consider this, if they were respectively g cos θ and g sin θ then the net acceleration would be the root-sum-square of these, giving g. I.e. it would accelerate down the ramp as fast as a dropping stone. Not possible unless the ramp is vertical.
So humour me: write out equations for the forces and accelerations.
 
  • #25
haruspex said:
I'm aware of that, and your expressions for horizontal and vertical accelerations are still wrong. Consider this, if they were respectively g cos θ and g sin θ then the net acceleration would be the root-sum-square of these, giving g. I.e. it would accelerate down the ramp as fast as a dropping stone. Not possible unless the ramp is vertical.
So humour me: write out equations for the forces and accelerations.

I see your point... But the acceleration is at the end of the ramp, as in, the moment right as it reaches the very end of the ramp. At that point, it WOULD have -9.8 as its' acceleration, and its' components would indeed be falling as fast as dropping a stone. This is why we chose to start off at that moment when it is at the end of the ramp so we can avoid the friction component of it altogether for the calculations (I have no idea how to calculate the friction at the moment anyway... We only just started the concept of forces recently in class. This problem was given to us before that chapter). We just need to find the height of the ramp, there's no need to over-complicate it.

But anyway, I'm still confused on what mfb was saying.

I found h to be:
h = 4.25t2*Sin(30)

But I'm not sure how to proceed from here.
 
Last edited:
  • #26
Shaku said:
But the acceleration is at the end of the ramp, as in, the moment right as it reaches the very end of the ramp. At that point, it WOULD have -9.8 as its' acceleration, and its' components would indeed be falling as fast as dropping a stone.
You need to find the velocity as it leaves the ramp, and for that the accelerations are those that apply all along the ramp.
How many times do I need to ask you to write out the force/acceleration equations?
 
  • #27
haruspex said:
You need to find the velocity as it leaves the ramp, and for that the accelerations are those that apply all along the ramp.
How many times do I need to ask you to write out the force/acceleration equations?

How would I figure out the force? The problem didn't give a weight. Fnet = ma would leave me with two variables again.

9qecnq.png
 

Attachments

  • help3.png
    help3.png
    3.1 KB · Views: 520
  • #28
Don't worry about the mass. Let it be m. It will cancel out later.
Your force diagram is wrong. Which way does the normal force act? There's no friction, so forget Fs (and anyway it would have been Fk). What's Fslide??
 
  • #29
haruspex said:
Don't worry about the mass. Let it be m. It will cancel out later.
Your force diagram is wrong. Which way does the normal force act? There's no friction, so forget Fs (and anyway it would have been Fk). What's Fslide??

30jqvx5.jpg


Sorry, I just recently started on forces. This new diagram should be correct, having no friction. Just Fn and Fg. -- The Fslide on the old diagram was just a mistake. I forgot that there are no forces acting on it since there are no forces which are physically touching the object (unless it's a long-range force).

Fnet = ma

Fynet = m(gSin(30))
Fxnet = m(gCos(30))

Is this correct? I'm not sure since you said gSin(30) & gCos(30) wasn't the acceleration... I don't know the force nor the mass to figure out acceleration if I needed to otherwise.
 

Attachments

  • help4.jpg
    help4.jpg
    3.2 KB · Views: 480
  • #30
Shaku said:
Fynet = m(gSin(30))
Fxnet = m(gCos(30))
The diagram is right now but those equations do not spring from it at all. What happened to the normal force? How does g get a horizontal component?
Let's try it again, one step at a time:
- what is the component of Fn in the vertical direction?
- what is the component of Fn in the horizontal direction?
- what is the component of Fg in the vertical direction?
- what is the component of Fg in the horizontal direction?
 

Similar threads

A ball climbing a ramp while "rolling the wrong way"
  • · Replies 32 ·
2
Replies
32
Views
3K
Friction Problem of a Crate Sliding Down a Ramp
  • · Replies 4 ·
Replies
4
Views
4K
Find Height of Ramp: H=1.0m, d=1.0m, θ=30°
  • · Replies 3 ·
Replies
3
Views
6K
Object slides down frictionless ramp. Find acceleration.
  • · Replies 3 ·
Replies
3
Views
9K
A steel washer suspended from the top of a crate sliding down a ramp.
  • · Replies 1 ·
Replies
1
Views
5K
What Is the Effect of Friction on the Height of a Sphere Rolling Down a Ramp?
  • · Replies 2 ·
Replies
2
Views
3K
How Does a Speck of Dust Affect the Motion of a Box on an Inclined Ramp?
  • · Replies 33 ·
2
Replies
33
Views
4K
Distance an object travels after sliding and falling from roof
  • · Replies 8 ·
Replies
8
Views
3K
How Much Work Does Friction Do on a Crate Sliding Down a Ramp?
  • · Replies 2 ·
Replies
2
Views
2K
What Are the Forces and Energy Involved in a Block Sliding Down a Ramp?
  • · Replies 4 ·
Replies
4
Views
4K