Sliding resistance of eccentrically loaded block

[hillbilly63]

Summary:: What is the sliding resistance of an eccentrically loaded block on a flat surface?

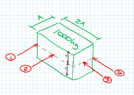
If a 1000kg block is placed on a flat surface (say coeff. of friction = 0.4), what force does it take to slide if it loaded eccentrically, i.e. at the far edge of the block?

My thinking is there is both rotation and translation to consider, but I can't come up with an answer that makes sense (at all!).

See the attached diagram - I 'know' that for force 2 & 3, the sliding resistance would be (1000x9.81/1000) x 0.4 = 3.92kN.

For forces 1 and 4 though, I'm scratching my head (a lot, and for quite some time now!). My intuition is also that force 1 would be lower than force 4, and both would be lower than 2 & 3.

(to clarify, the arrows are illustrating different load positions, not simultaneous loads)

 

[jbriggs444]

If a 1000kg block is placed on a flat surface (say coeff. of friction = 0.4), what force does it take to slide if it loaded eccentrically, i.e. at the far edge of the block?

To make sure that I am imagining it correctly, you have a block on top of a table.

If you push it dead center on one of the vertical faces, it will move in the direction of the applied force. For a 1000 kg block with a coefficient of friction of 0.4, that is 400 kilograms-force (about 4000 N).

But now you apply a force in the same direction, but at the edge of the left or right edge of the face rather than in the center. One would expect the block to both move and rotate as a result.

You want to know how hard you have to push before it will budge.

This strikes me as quite a challenging exercise. I would start by trying to view the resulting motion as a rotation about an unknown fixed point. The solution will entail determining that unknown fixed point. It will also require making an assumption about the pattern of vertical pressure of block on table.

 

[hillbilly63]

Yes, you are visualising it correctly. I'm glad you agree it isn't a trivial question, it's been taxing me for some time! It isn't a homework question, I'm a Structural Engineer, but the moderators moved the question to here.

The real life scenario is temporary fence posts bolted to the side of concrete kentledge blocks. In real life the load is applied above the centre of block mass, so the actual behaviour is even more complicated as the pressure distribution on the base will vary due to overturning effects. But I simplified it for now.

I paid someone on Freelancer to analyse it using Ansys but their answers were nonsensical so I have lost faith in them!

 

[haruspex]

Suppose that when the block starts to slide it will rotate about some point O. Sliding will occur everywhere except O at once, so all points reach the limit of static friction at the same time.
Let the weight per unit area be w. For an area element dA the normal force is $wdA$ and the limiting friction force $w\mu_sdA$. If dA lies on a circle radius r about O then this force will be tangential to the circle and exert a torque $rw\mu_sdA$ about O. Integrating these torques (tricky because the larger circles are incomplete) gives the total torque resistance to the applied force.
What do you think determines where O will be?

 

[jbriggs444]

Thank you, @haruspex. That is the approach that I had in mind.

For added fidelity, if we factor in the fact that the push is not at ground level, we have to worry about the possibility that the normal force is disproportionately slewed because of torque about a horizontal axis.

Edit: hmmm. but if the center of rotation is somewhere on the centerline and we assume a linear slew for normal force then that effect cancels out nicely leaving no impact on the required torque for a given circular ring.

Double edit: But the result will include a tendency for the brick to shift leftwards under a force on the left edge. So the center of rotation will not be on the center line.

 

[haruspex]

if we factor in the fact that the push is not at ground level

That gets very tricky because we have to consider how the block deforms. In the original we could just assume it was sufficiently floppy that the vertical load would be spread uniformly. I think it could be solved by taking the block to have a uniform flexural modulus, but that's quite a challenge in itself.
One extreme case does get easier, though. If the block is on the point of tipping before it slides then all the frictional forces lie on the far edge of the base.

 

[Lnewqban]

...
The real life scenario is temporary fence posts bolted to the side of concrete kentledge blocks.

Does the temporary fence load the concrete block with anything close to 3.92kN?

 

[haruspex]

Does the temporary fence load the concrete block with anything close to 3.92kN?

Pushing at one end won't require quite as much force. If we pretend the block is long and thin then I calculate the force needed is only $\sqrt 2-1$ times as much.

 

[hillbilly63]

Does the temporary fence load the concrete block with anything close to 3.92kN?

Yes. It's a solid fence, and block spacing needs to be as efficient as possible, so understanding the exact sliding force (or a reasonable approximation of it) is necessary.

 

[hillbilly63]

That gets very tricky because we have to consider how the block deforms. In the original we could just assume it was sufficiently floppy that the vertical load would be spread uniformly. I think it could be solved by taking the block to have a uniform flexural modulus, but that's quite a challenge in itself.
One extreme case does get easier, though. If the block is on the point of tipping before it slides then all the frictional forces lie on the far edge of the base.

The block is concrete, so I don't envisage much deformation. You have touched upon the complexities of the problem when including overturning effects, hence why I simplified it initially, just to get a sense for the effect of eccentricity.

 

[haruspex]

Yes. It's a solid fence, and block spacing needs to be as efficient as possible, so understanding the exact sliding force (or a reasonable approximation of it) is necessary.

How tall is the fence and at what height do you anticipate the applied force?

 

[hillbilly63]

The responses have confirmed my feeling the behaviour is very complex, and the best way to verify sliding resistance is to do some FE modelling on something like Solidworks, but I don't have such software. It would be good to have a hand-calc idea of what one should expect to verify the analysis output is valid. Failing that, I think doing some real life tests might be in order.

Thanks all for the input. If anyone has access to Solidworks or similar and fancy's running the simulation, I'd be very interested (and grateful!)

 

[hillbilly63]

How tall is the fence and at what height do you anticipate the applied force?

Typically the fence would be 2.4m high, with resultant force applied mid-height of post (i.e. 1.2m above ground level)

 

[haruspex]

Typically the fence would be 2.4m high, with resultant force applied mid-height of post (i.e. 1.2m above ground level)

Based on that and the image in post #1, I'm guessing the blocks are about 660mm wide. So it would take a lateral force of 3.9kN at height 1.2m to topple it.
The thin line approximation in post #8 is probably a lower bound for the force to slide it if applied at one end, i.e. 1.6kN.

 

[hillbilly63]

Based on that and the image in post #1, I'm guessing the blocks are about 660mm wide. So it would take a lateral force of 3.9kN at height 1.2m to topple it.
The thin line approximation in post #8 is probably a lower bound for the force to slide it if applied at one end, i.e. 1.6kN.

Thanks haruspex. Block spacing (and therefore number of blocks) has a significant impact on cost as it's not just the blocks themselves, its transporting them, fixing posts to them etc. so there is motivation to find the upper bound to achieve maximum spacing!

 

[haruspex]

Thanks haruspex. Block spacing (and therefore number of blocks) has a significant impact on cost as it's not just the blocks themselves, its transporting them, fixing posts to them etc. so there is motivation to find the upper bound to achieve maximum spacing!

This seems to have gone in another direction. I saw nothing earlier about block spacing.
The typical use I see is sections of fence each having a post at each end. One post goes into one end of a concrete block, and one post of the next section goes in the other end of that block.
If that is not your set up, please clarify. And what are you able to vary to reduce the number of blocks, section length?

 

[hillbilly63]

This is a typical arrangement (although note here the post is mounted to the front). This is for construction site perimeter fencing.

 

[Lnewqban]

Yes. It's a solid fence, and block spacing needs to be as efficient as possible, so understanding the exact sliding force (or a reasonable approximation of it) is necessary.

In that case, you may want to consider the anchoring of the fence posts to the concrete block offering some degree of resistance against rotation of the blocks respect to the structure of the fence.

Also, only one finite section of the fence will be acting on one block.
Then, the integrity of the fence to withstand wings strong enough to transfer the maximum calculated load to the block via anchors.

Perhaps, building some horizontal net of cable bracing among the blocks could remove a lot of moment from the fence-block anchors and significantly reduce the concern on rotation induced by off-center loads.

If feasible, locating the blocks on both sides of the fence would increase the margin on tip-over of the whole fence.

 

[hillbilly63]

This is a typical arrangement (although note here the post is mounted to the front). This is for construction site perimeter fencing.

View attachment 298556

In that case, you may want to consider the anchoring of the fence posts to the concrete block offering some degree of resistance against rotation of the blocks respect to the structure of the fence.

Also, only one finite section of the fence will be acting on one block.
Then, the integrity of the fence to withstand wings strong enough to transfer the maximum calculated load to the block via anchors.

Perhaps, building some horizontal net of cable bracing among the blocks could remove a lot of moment from the fence-block anchors and significantly reduce the concern on rotation induced by off-center loads.

If feasible, locating the blocks on both sides of the fence would increase the margin on tip-over of the whole fence.

The connection between rail and post would be the critical point in resisting rotation. Unfortunately the narrow face of the post means high leverage giving large tension forces on the screws. This is additive to the tension in the screws due to the wind load. End result: likely not feasible.

Bracing the blocks using cables is too complex for this kind of structure, and likely too vulnerable to damage/abuse on a construction site.

I think the most promising solution is to connect the block on the side opposite the post to the bottom horizontal rail.

But I still want to know when the block will slide due to eccentric loading!

 

[jbriggs444]

But I still want to know when the block will slide due to eccentric loading!

When theory does not provide the answer (or even when it does), there is always experiment.

You can buy a spring scale for $30 (USD) or so. Or one could go cheaper with some string (that stuff one uses to snap blue lines should work), a tape measure, a reference weight and some trigonometry.

 

[haruspex]

This is a typical arrangement (although note here the post is mounted to the front). This is for construction site perimeter fencing.

View attachment 298556

That picture leaves me wondering what force you were concerned about in post #1.
The principal forces from the fence should act through the midlines of the blocks, no? A force as shown in post #1 would be parallel to the fence, yes?
Anyway, I suggest my result in post #14 should be good enough for that case, while providing some safety margin.

If wind is the issue, https://www.engineeringtoolbox.com/wind-load-d_1775.html has a formula for the pressure on the fence. But it does not give the average height of that pressure, which is what you need to know for working out whether the blocks might tip over. https://www.jcu.edu.au/__data/asset...ads-on-Fences-and-Hoardings.pdf/_noproxycache suggests the centre of pressure is no higher than 60% of the full height. It also considers the angle of attack of the wind.