Solution for f(n) in recurrence equation

[Bruno Tolentino]

Exist solution for SAR(n+1) in this equation:

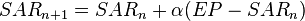
https://en.wikipedia.org/wiki/Parabolic_SAR

?

I want to eliminate SAR(n), but I never saw this kind of equation before...

 

[fresh_42]

If you substitute $SAR_n$ by $SAR_n = SAR_{n-1}+\alpha (EP-SAR_{n-1})$ and so on, you will get the following (where I substituted $n+1$ by $n$ and if I made no mistake):
$$SAR_{n}=(1-\alpha)^{n}SAR_0+(1-(1-\alpha)^{n})EP$$