Solve 2 Loop RC Circuit: Find Q(topen)

[acrimius]

1. Situation and Variables:
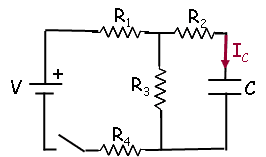
A circuit is constructed with four resistors, one capacitor, one battery and a switch as shown. The values for the resistors are: R1 = R2 = 30 Ω, R3 = 66 Ω and R4 = 113 Ω. The capacitance is C = 64 μF and the battery voltage is V = 12 V. The positive terminal of the battery is indicated with a + sign.

2. Sub-question:
After the switch has been closed for a very long time, it is then opened. What is Q(t_open), the charge on the capacitor at a time t_open = 786 μs after the switch was opened?

3. Relevant Equations:
Kirchhoff's Loop Rule: \Sigma V_l = 0

Kirchhoff's Node Rule: I_i = I_o

V_C = \frac {q} {C}

For a discharging circuit:
q(t) = q_o e^\frac {-t} {\tau}

4. Attempt:
When the switch is closed initially and time goes to infinity, the capacitor charges up and reaches it's capacitance, which I found the max charge, q_o to be about 243μC.
Then for a discharging circuit, we have the equation I gave above q(t). I believe my issue is finding tau, which is RC. I have been using R = R_1+R_2 but that hasn't been correct. I've tried different combinations of resistors but I'm not quite getting it.

 

[NascentOxygen]

Show your working for the capacitor charging voltage.

How to determine the capacitor's discharging path when the switch is an open circuit?

 

[acrimius]

Show your working for the capacitor charging voltage.

How to determine the capacitor's discharging path when the switch is an open circuit?

Q(∞)?
I_C = 0 ∴ I₁ = I₂
Knowing this:
Loop for right hand side (I):
\frac {q} {C} = I_2R_3

Loop for left hand side (II):
V_b = I_2(R_1+R_3+R_4)
Therefore,
I_2 = \frac {V_b} {R_1+R_3+R_4}

plugging this into (I):
\frac {q} {C} = \frac {V_bR_3} {R_1+R_3+R_4}

then solve for q, which is just multiplying both sides by C.
The exactly answer they have for Q is 242.526315789474μC, which is what I got, and I have this number stored so I used it for my text calculation of find Q(786μs) from the equation q(t) = q_oe^\frac{-t} {\tau}

 

[acrimius]

Also I figured the current go across the switch, so I assumed it would only traverse the right hand side, which is why I use R=R_2+R_3 the equation I originally posted is not what I had written, it was a typo on my part.

 

[NascentOxygen]

which is why I use R=R_2+R_3

That's the discharge path. So you need to be able to write by inspection the exponential time equation for the capacitor voltage as it discharges. I see you almost have.

Are you able to calculate τ and finish this now?

 

[acrimius]

That's the discharge path. So can you write by inspection the exponential time equation for the capacitor voltage as it discharges?

Right. So I have this equation:
q(t) = q_oe^\frac {-t} {R_2+R_3}
but because R₂+R₃ is so large in comparison to t=786μs, the e part is approximately 1, and so my calculator outputs nearly the same answer as I had before, which the website counts as incorrect

 

[NascentOxygen]

The time constant is the product of R and C. It needs to have units of seconds, or it wouldn't be a time.

 

[acrimius]

The time constant is the producut of R and C.

Wow, that was a really dumb mistake on my part. Thanks for helping me though, I probably would have never realized that.

 

[NascentOxygen]

I thought you had it right in your first post ...

I believe my issue is finding tau, which is RC.