Solve Pedagogical Machine Homework

[PFuser1232]

Homework Statement

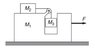
A “pedagogical machine” is illustrated in the sketch (attached image). All surfaces are frictionless. What force $F$ must be applied to $M_1$ to keep $M_3$ from rising or falling?

Homework Equations

$$\sum_{}^{} \vec{F} = m \vec{a}$$

The Attempt at a Solution

I have chosen a coordinate system such that all particles have positive coordinates. My $x$-axis points to the right and my $y$-axis points upwards. The length of the rope remains constant, and it can be expressed as:
$$l = x_p - x_2 + \frac{\pi R}{2} + y_p - y_3$$
The pulley is located at $(x_p,y_p)$.
Differentiating twice with respect to time and rearranging:
$$\ddot{x}_2 + \ddot{y}_3 = \ddot{x}_p$$
Since the pulley and $M_1$ are fixed:
$$\ddot{x}_2 + \ddot{y}_3 = \ddot{x}_1$$
Since $\dot{y}_3 = 0$ for all $t$, $\ddot{y}_3 = 0$.
In other words:
$$\ddot{x}_1 = \ddot{x}_2$$
Now, applying Newton's second law to each mass:
$$T - M_3 g = 0 ⇒ T = M_3 g$$
$$T = M_2 \ddot{x}_2$$
$$F - T = M_1 \ddot{x}_1$$
Where $T$ is the tension in the rope.
$$M_3 g = M_2 \ddot{x}_2 ⇒ \ddot{x}_2 = \frac{M_3 g}{M_2} = \ddot{x}_1$$
$$F = T + M_1 \ddot{x}_1 = M_3 g (1 + \frac{M_1}{M_2})$$
$$F = M_3 g \frac{M_1 + M_2}{M_2}$$
Which doesn't match the clue given in my book. According to my book, if all three masses are equal, then $F = 3Mg$.
Where did I go wrong?

 

[haruspex]

How do you get your equation $F-T=M_1\ddot x_1$? What are the forces acting on M₁?

 

[PFuser1232]

How do you get your equation $F-T=M_1\ddot x_1$? What are the forces acting on M₁?

In the $x$-direction, there's $F$ and $T$.
$T$ acts on the pulley, which is a part of $M_1$.
All surfaces are frictionless.

 

[haruspex]

In the $x$-direction, there's $F$ and $T$.
$T$ acts on the pulley, which is a part of $M_1$.
All surfaces are frictionless.

Yes, but you've missed a force. What makes M₃ accelerate?

 

[PFuser1232]

Yes, but you've missed a force. What makes M₃ accelerate?

The net force caused by the difference between $N$ and $N'$ (different normal reactions)?

 

[PFuser1232]

The net force caused by the difference between $N$ and $N'$ (different normal reactions)?

$$\vec{F}_{31} = -\vec{F}_{13}$$
The net force on $M_3$ is to the right, so the force $M_3$ exerts on $M_1$ must be to the left.
I guess I missed an additional constraint:
$\ddot{x}_1 = \ddot{x}_3$ since $x_3$ and $x_1$ differ by a constant.
I got the right answer, thanks!
I have a question though, the equation only holds if $M_3$ is always in direct contact with $M_1$, right?
I have not taken into account the fact that $M_3$ can swing left and right while deriving the first constraint equation.

 

[haruspex]

$$\vec{F}_{31} = -\vec{F}_{13}$$
The net force on $M_3$ is to the right, so the force $M_3$ exerts on $M_1$ must be to the left.
I guess I missed an additional constraint:
$\ddot{x}_1 = \ddot{x}_3$ since $x_3$ and $x_1$ differ by a constant.
I got the right answer, thanks!
I have a question though, the equation only holds if $M_3$ is always in direct contact with $M_1$, right?
I have not taken into account the fact that $M_3$ can swing left and right while deriving the first constraint equation.

Yes, if the two do not start quite in contact then there will be a different behaviour initially, but it wouldn't last long.