Solve Snell's Law: Glass Cube Refractive Index = 1.77

[DylanXO]

Homework Statement

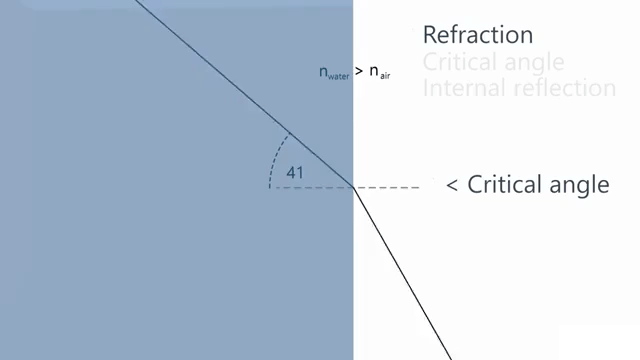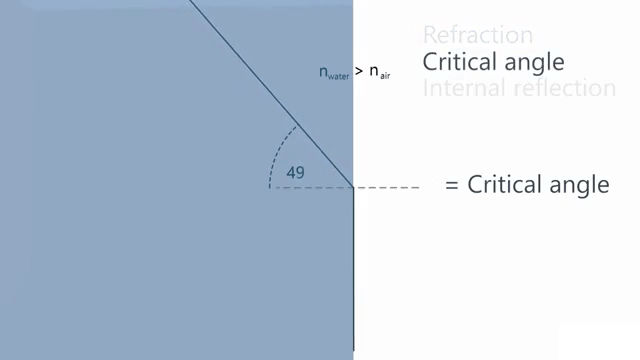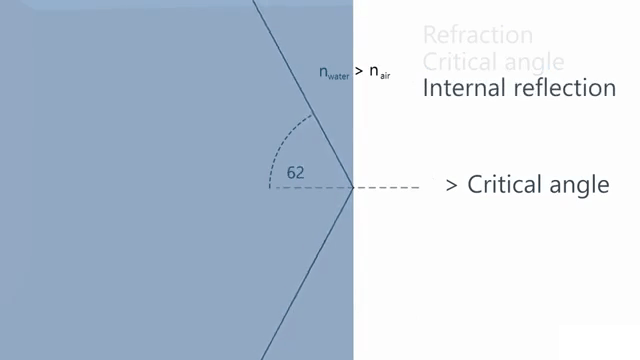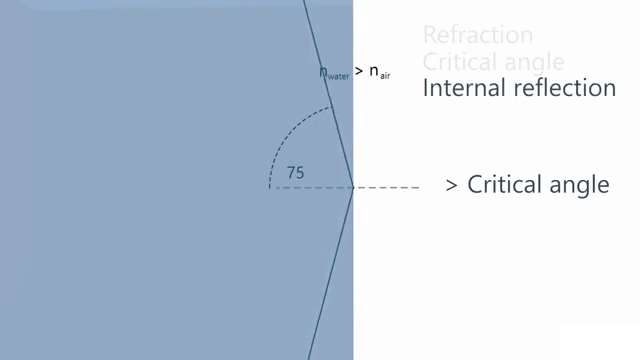
A ray of light is traveling in a glass cube that is totally immersed in water. You find that if the ray is incident on the glass-water interface at an angle to the normal greater than 48.7°, no light is refracted into the water. Calculate the refractive index of the glass.

Homework Equations

Snell's Law:

Refractive Index of Water: 1.33

The Attempt at a Solution

Na = Nb*Sin(Θb)/Sin(Θa)
Na = 1.33*Sin(90°)/Sin(48.7°)
Na = 1.77
Glass Cube Refractive Index = 1.77

I feel that I have made an error or that I'm not grasping the concept correctly. Any guidance or explanation would be highly appreciated.

 

[mjc123]

No, it looks right to me. What makes you think it isn't?

 

[Doc Al]

This looks good to me. This phenomenon is called total internal reflection, in case you want to explore it a bit.

 

[renec112]

...I feel that I have made an error or that I'm not grasping the concept correctly...

Seems correct to me as well. glasses refractive indices are typically around that value. Any part of the concept you are confused about?

 

[DylanXO]

This looks good to me. This phenomenon is called total internal reflection, in case you want to explore it a bit.

Thank you, I think some additional reading on that will help resolve any confusion I'm having.

 

[DylanXO]

Seems correct to me as well. glasses refractive indices are typically around that value. Any part of the concept you are confused about?

It was more the result itself from textbooks I have checked and a quick look online, it seemed that the indices for glass were lower. Although I understand now, that the indices for glass are varying.

 

[joaopcnogueira]

The incidence angle 48.7º in this case, is the critical angle, i.e, the angle which makes the refraction angle 90º. We know that because in the statement of the problem, we can read the following:

[..] You find that if the ray is incident on the glass-water interface at an angle to the normal greater than 48.7°, no light is refracted into the water.

The fact that for any angle greater than 48.7º no light is refracted into the water, means that 48.7º is the critical angle and the refraction angle is 90º.

That is the reason you have used 90º into the Snell's Law.

Reference: https://en.wikipedia.org/wiki/Total_internal_reflection

 

[renec112]

It was more the result itself from textbooks I have checked and a quick look online, it seemed that the indices for glass were lower. Although I understand now, that the indices for glass are varying.

I forgot i once made this animation about it:

It's showing a light ray going from water (bigger index) to air(lower index) - an example where internal reflection can happen.

 

[joaopcnogueira]

I forgot i once made this animation about it:

It's showing a light ray going from water (bigger index) to air(lower index) - an example where internal reflection can happen.

Amazing animation, thanks for share!