so_gr_lo
- 69
- 10
- Homework Statement
- Hi,
I have included an attachment of the question about differential equations. I found a similar question and solution on this website:
https://doubtnut.com/question-answer/a-tangent-at-a-point-p-on-the-curve-cuts-the-x-axis-at-a-and-b-is-the-foot-of-perpendicular-from-p-o-262330
- Relevant Equations
- Given differential equation:
xdy/dx = 2y
Here is my attempt at a solution:
y = f(x)
yp - ym = dy/dx(xp-xm)
ym = 0
yp = dy/dx(xp-xm)
xm=ypdy/dx + xm
xm is midpoint of OT
xm = (ypdy/dx + xm) /2
Not sure where to go from there because the solution from the link uses with the midpoint of the points A and B intersecting the x-axis, whereas the assignment question concerns the points M and T on the x-axis, where M is the midpoint between the origin and T. Can anybody give any clues?
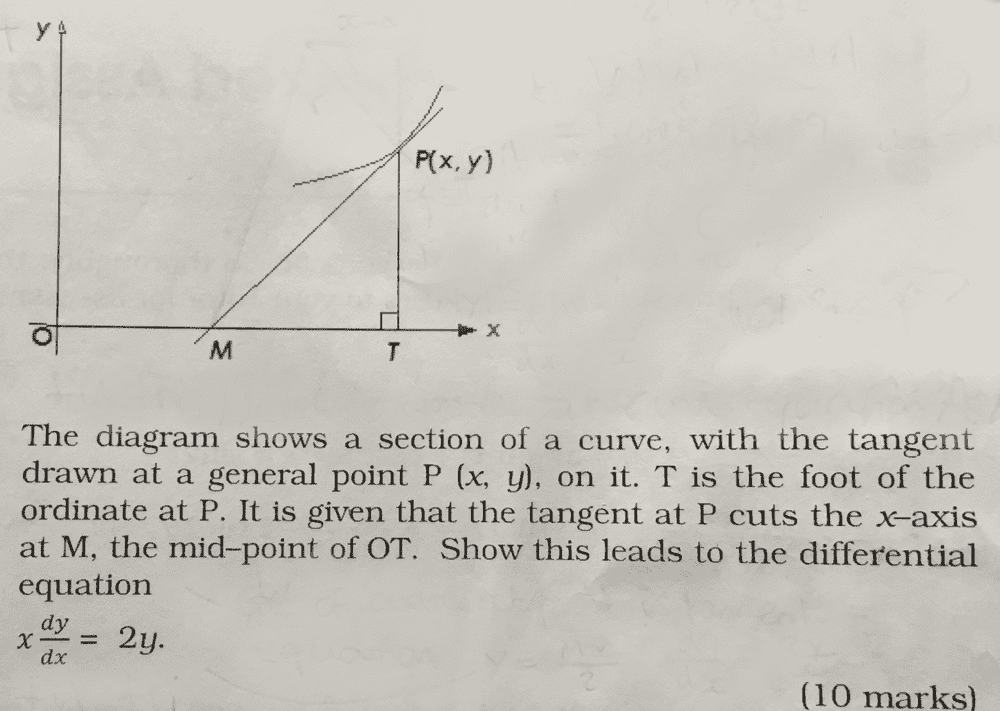
y = f(x)
yp - ym = dy/dx(xp-xm)
ym = 0
yp = dy/dx(xp-xm)
xm=ypdy/dx + xm
xm is midpoint of OT
xm = (ypdy/dx + xm) /2
Not sure where to go from there because the solution from the link uses with the midpoint of the points A and B intersecting the x-axis, whereas the assignment question concerns the points M and T on the x-axis, where M is the midpoint between the origin and T. Can anybody give any clues?
Last edited by a moderator:
