Tevion
- 21
- 0
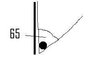
A mass 0.15kg sits in a corner between a vertical wall and a lift, that makes an angle of 65° with the wall. The only force acting on the mass is its weight (W), its normal reaction (Nr) from the lift and its normal reaction (Nw) from the wall. The mag of the acceleration due to gravity to be g = 10ms^2
1) Show that the angle between the directions of the forces W and Nr, is 155°
2) Draw a force diagram for the forces acting on the mass, giving the sizes of the angles between the forces
3) Draw a corrresponding triangle of forces, giving the sizes of angles
4) Use the triangle of forces to find the magnitudes of the two normal reactions in Newtons
Any help with the above would be most appriciated.
Thanks
1) Show that the angle between the directions of the forces W and Nr, is 155°
2) Draw a force diagram for the forces acting on the mass, giving the sizes of the angles between the forces
3) Draw a corrresponding triangle of forces, giving the sizes of angles
4) Use the triangle of forces to find the magnitudes of the two normal reactions in Newtons
Any help with the above would be most appriciated.
Thanks