kstorm19
- 4
- 0
Homework Statement
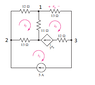
The problem asks to solve for i1, i2, and i3 using the mesh method in the following circuit:

I will also include the link, because I noticed I am having trouble attaching the image to the post: https://imgur.com/a/bBvuLXM
I would also like to confirm the answer by solving using the node analysis.

2. Homework Equations
V=IR
The Attempt at a Solution
First of all, I solved for all three currents using the mesh analysis.
i1 = 5 A
For mesh 2, this is the equation I came up with:
12i2 + 11(i2-i3) + 13 (i2-i1) = 0
And so, using the Node 3:
i3 = 5+ 1/3 Vx
But Vx = 13i3
So i3 = 5 + 13/3 i3
i3= -1.5 A
Going back to equation for mesh 2 and solving for i2:
i2= -1.35 A
So I have:
i1 = 5 A
i2= -1.35 A
i3= -1.5 A
I wanted to confirm these results using the node analysis.
For node 1
(V1-V2)/12 + V1/11 + (V1-V3)/13 = 0
For node 2
(V2-V1)/12 + V2/13 = 5
For node 3
(V3-V1)/13 + 1/3 Vx + 5 = 0
So in this last equation I got a little confused, since when I was setting it up, V3 has the highest potential. If Vx = V1-V3 by looking at the arrow, should I write it that way in the equation, or should I put instead V3-V1?
I figured that maybe it should be written using V3-V1, so this is how I wrote the equation for node 3:
(V3-V1)/13 + 1/3 (V3-V1) + 5 = 0
Solving these 3 equations, I got:
V1 = 6.036 V
V2 = -0.061 V
V3 = -18.23 V
Now, replacing for Vx, which should be -19.5 V since Vx = 13i3 and i3=-1.5 A, I don't get that answer.
I also tried (V3-V1)/13 + 1/3 (V1-V3) + 5 = 0 for the third node equation in case I was wrong and I got:
V1 = -6.64 V
V2 = -3.21 V
V3 = 12.58 V
Now, subtracting V1-V3 gets me -19.22 V (almost -19.5 V from the mesh analysis).
But looking to confirm that i2=-1.35 A, (V2-V1)/12 doesn´t get me anywhere near that value. Where did I go wrong?
Thank you so much guys for your time and help.
Attachments
Last edited by a moderator: