karush
Gold Member
MHB
- 3,240
- 5
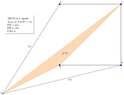
View attachment 5803
I tried about an hour to solve this but couldn't get the ratios to work I assume there are isoseles triangles in this but that is just observation
I tried about an hour to solve this but couldn't get the ratios to work I assume there are isoseles triangles in this but that is just observation