Solving a Problem With Fourier Transforms: Heaviside Unit Step Function

[Telemachus]

Hi there. I'm starting with the Fourier transforms, and I'm having some trouble with my first exercise on this topic.
The problem says: Given $$f(x)=H(x)-H(x-l)$$ (H(x) is the Heaviside unit step function).
a) Consider the odd extension for f and find its Fourier integral representation.
b) Using the previous incise calculate the value for $$\int_0^{\infty}\frac{1-cos (\omega l)}{\omega}\sin (\omega l) d\omega$$

Well, for a) I think I should get the Fourier transfor for the sign function, I don't know if this is right, but anyway I've defined the function like this:

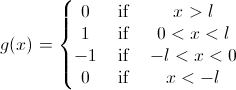
Then the Fourier integral representation:
$$g(x)=\displaystyle\frac{1}{2\pi}\displaystyle\int_{-\infty}^{\infty}\displaystyle\int_{-\infty}^{\infty}g(x)e^{-i \omega x}dx e^{i \omega x}d\omega$$

But g(x) is odd, then:

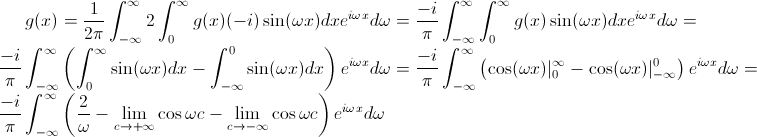
And the thing is that the integral for the cosine diverges as I see it, but I'm probably doing something wrong.

Help please :)

PD, I don't know why latex isn't working in some cases, so I've attached some images.

 

[jbunniii]

Can you tell us how your g(x) is related to the f(x) in the problem statement?

Also, is there any assumption regarding whether $l$ is positive, negative, or zero?

If $l$ is positive, then f(x) should be 1 for $0 < x < l$ and 0 elsewhere. (Change $<$ to $\leq$ as appropriate, depending on how you defined the Heaviside function.)

P.S. Your Latex looks fine, but be aware that it doesn't seem to render correctly in your own browser after you first post it. If you refresh the page, it should fix itself.

 

[Telemachus]

Hi jbunni. Thanks for posting.

Can you tell us how your g(x) is related to the f(x) in the problem statement?

Yes, g(x) is the odd extension for f(x). Here you have a graph of both, I take l=2, but l is arbitrary (I think that when I find the Fourier Integral I must be doing something like l->infinity, so I think I should get the sign function):

You're right about that it must be 1 at x=0. But it doesn't make any difference I think.

About latex, I've realized that sometimes I have to refresh to see the "pictures" instead of the code, but today it just didn't work, and for some commands (the brackets for example, to define a trunked function) it just doesn't work for me, I've tried to refresh, but it didn't work, so then I've uploaded the pictures.

 

[Telemachus]

The odd function can be also defined as $$g(x)=H(x)-H(x-l)-H(-x)+H(-x-l)$$