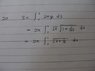Integrating Trigonometric Functions: How to Remember and Use Identities?
- Thread starter athrun200
- Start date
-
- Tags
- Integrals
Click For Summary
The discussion focuses on challenges with integrating trigonometric functions and remembering relevant identities. Participants emphasize the importance of key identities, such as the Pythagorean identity sin² + cos² = 1 and half/double angle formulas, for solving integral problems. A resource link for hyperbolic identities is shared to aid memory retention. The conversation highlights that the identities one should remember may vary based on the specific mathematical context or class. Overall, the thread addresses both integration techniques and strategies for memorizing trigonometric identities.
Similar threads
- · Replies 8 ·
- · Replies 18 ·
- · Replies 10 ·
- · Replies 11 ·