Solving for Center of Mass in a Bent Wire: xcm and ycm Values Explained

Click For Summary

Homework Help Overview

The discussion revolves around calculating the center of mass (xcm and ycm) for a wire bent into a specific shape, with a focus on understanding the contributions of different segments of the wire. The problem is situated in the context of mechanics and involves concepts related to mass distribution and geometry.

Discussion Character

  • Mixed

Approaches and Questions Raised

  • Participants explore treating the wire as two separate rods to find their respective centers of mass. There is a suggestion to visualize the problem as a two-particle system, with questions about the correctness of calculated values for xcm and ycm. Some participants express uncertainty about their answers and seek clarification on the calculations involved.

Discussion Status

The discussion is ongoing, with various approaches being suggested. Some participants have provided partial calculations and are questioning their accuracy. There is a mix of confirmed values and requests for further verification, indicating an active exploration of the problem without a clear consensus on the final answers.

Contextual Notes

Participants mention the need for additional hints and the importance of considering the different masses of the vertical and horizontal rods. There is also a reference to a visual aid that may assist in understanding the problem setup.

squintyeyes
Messages
44
Reaction score
0
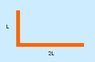
A wire of uniform density is bent into the shape shown in the figure below.

The value of L is 0.740 cm. Answer the following questions assuming that the origin is at the bottom left corner.

What is the value of xcm?
cm

What is the value of ycm?
cm

Attempt
xcm = 2*.74 = 1.48 cm

ycm = .74 cm

I get the feeling that this is wrong.
 

Attachments

  • center of mass.jpg
    center of mass.jpg
    2.6 KB · Views: 420
Physics news on Phys.org
First of all, treat this as 2 separate rods. Find the center of the vertical rod, and find a center of horizontal rod.

Now redraw this problem as a 2 particle problem, where each particle is located at the center of each rod. For the vertical rod, the center is at (0,L/2), and for horizontal rod the center is at (2L/2,0). Now you have 2 particles and you can find a distance between them.

I'll attach the picture but you are going to have to do all the calculations to get actual coordinates. Use it as a visual aid.

Also I'm sure you won't be able to solve this without one more hint: think about the horizontal vs vertical rod. They are not of the same mass, hence the point particles are not of same mass.
 
Last edited:
the answer i put for the first part was 0.493 and it was right. But for the secound part i got 0.493 as well is that right? i am not sure and really need an answer fast.
 
squintyeyes said:
the answer i put for the first part was 0.493 and it was right. But for the secound part i got 0.493 as well is that right? i am not sure and really need an answer fast.

Post your work. Refer to my graph I already gave you the center of mass, for y its between 0.1 and 0.15.
 
thanks for all your help! i just forgot to divide by two
 

Similar threads

Displacement of Center of Mass Problem
  • · Replies 3 ·
Replies
3
Views
3K
Kinetic energy in center of mass reference frame
  • · Replies 3 ·
Replies
3
Views
2K
Need help finding center of mass of a molecule.
  • · Replies 14 ·
Replies
14
Views
5K
What is the center of mass if square D is placed on top of square B?
  • · Replies 2 ·
Replies
2
Views
2K
Formally finding the center of mass
  • · Replies 13 ·
Replies
13
Views
7K
Where Is the Center of Gravity of a Plywood Sheet with a Quadrant Removed?
  • · Replies 3 ·
Replies
3
Views
14K
Center of mass of a solid hemisphere (where's the error)?
  • · Replies 3 ·
Replies
3
Views
6K
Moment of inertia with system of rods
  • · Replies 2 ·
Replies
2
Views
1K
Find the center of mass of a plate
  • · Replies 57 ·
2
Replies
57
Views
6K
Tricky center of mass question
  • · Replies 11 ·
Replies
11
Views
4K